Question

Prove that if chords of congruent circles subtend equal angles at their centres then the chords are equal.

Answer 1

Hint: We will use the concept of circles to solve the problem. We will be be using the fact that congruent circles have equal radius then we will apply congruence between both the triangles and prove them congruent and hence deduce that the angle will be equal in both the triangles by the corresponding part of the congruent triangles.

Complete step-by-step answer:

We have been given two congruent circles and we have to prove that if their chords are equal then the angle they subtend at the centre are also equal.
Now we know that the congruent circles have equal radius therefore we draw a figure as per the question.

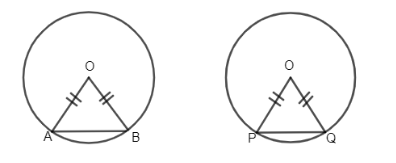
So, now we have been given that the chords AB and PQ subtends equal angle at the centre. So we have $\angle AOB=\angle POQ$ ….............................(1)
Now we will prove congruency in $\Delta OAB$ and $\Delta OPQ$.
$\angle OAB=\angle POQ$ ( from (1))
$AO=PO$ ( radii is same)
$OB=OQ$
So, we know that by SAS (side angle side) congruency $\Delta OAB$ and $\Delta OPQ$ are congruent.
Now, we know that by corresponding part of congruent triangles we have $AB=PQ$ .
Hence, chords are equal.

Note: To solve such a type of question one must have a good understanding of circles and its properties also one must know basic congruence like SAS etc.