Question

Prove that from any point $P\left( a{{t}^{2}},2at \right)$ on the parabola ${{y}^{2}}=4ax$ , two normal can be drawn and their feet Q and R have the parameters satisfying the equation${{\lambda }^{2}}+\lambda t+2=0$.

Answer 1

Hint: In this question, we can use the equation of the normal to the given parabola in the parametric form is $y+tx=2at+a{{t}^{3}}$, where t is a parameter.

Complete step-by-step answer:
Let us assume that $Q\left( a{{\lambda }^{2}},2a\lambda \right)$ be a point on the parabola ${{y}^{2}}=4ax$

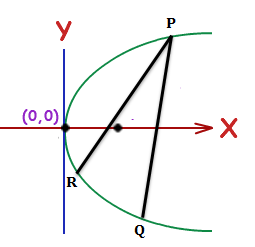
The equation of the normal to the given parabola in the parametric form is given by$y+\lambda x=2a\lambda +a{{\lambda }^{3}}.........................(1)$ where $\lambda $ is a parameter.
It passes through the point$P\left( a{{t}^{2}},2at \right)$, satisfying the equation (1) and we get
$(2at)+\lambda (a{{t}^{2}})=2a\lambda +a{{\lambda }^{3}}$
Rearranging the terms, we get
$2at+\lambda a{{t}^{2}}-2a\lambda -a{{\lambda }^{3}}=0$
Dividing both sides by a, we get
$2t+\lambda {{t}^{2}}-2\lambda -{{\lambda }^{3}}=0$
Taking common terms $\lambda $ from second and fourth terms and 2 form first and third terms, we get
 $2\left( t-\lambda \right)+\lambda \left( {{t}^{2}}-{{\lambda }^{2}} \right)=0$
Applying the formula ${{a}^{{2}}}-{{b}^{2}}=(a+b)(a-b)$ on the left side, we get
$2\left( t-\lambda \right)+\lambda \left( t+\lambda \right)\left( t-\lambda \right)=0$
Taking common terms $(t-\lambda )$ on the left side, we get
$\left( t-\lambda \right)\left[ 2+\lambda \left( t+\lambda \right) \right]=0$
Therefore, $\left( t-\lambda \right)=0\text{ or }\left[ 2+\lambda \left( t+\lambda \right) \right]=0$
$\text{t=}\lambda \text{ or }\left( {{\lambda }^{2}}+t\lambda +2 \right)=0$
But $t\ne \lambda $
$\left( {{\lambda }^{2}}+t\lambda +2 \right)=0$
Hence, $\lambda $ is the root of the equation $\left( {{\lambda }^{2}}+t\lambda +2 \right)=0$
Therefore, the points Q and R have the parameters satisfying the equation${{\lambda }^{2}}+\lambda t+2=0$.
Note: The equation ${{\lambda }^{2}}+\lambda t+2=0$ has real and distinct roots if ${{t}^{2}}-4\cdot 2>0\Rightarrow a{{t}^{2}}>8a$. So, the abscissa of the point P must exceed 8a for two distinct normal.