Question

Prove that for any two sets A and B $A=\left( A\bigcap B \right)\bigcup \left( A-B \right)$

Answer 1

Hint: Use the fact that $A-B=A\bigcap {{B}^{c}}$ and apply distributive law of union over the intersection of sets, i.e. $A\bigcup \left( B\bigcap C \right)=\left( A\bigcup B \right)\bigcap \left( A\bigcup C \right)$. Use $B\bigcup {{B}^{c}}=U$, where U is the universal set and use the fact that if $A\subset B$ then $A\bigcap B=A$. Simplify the above expression using these properties of intersection and union of sets.


Complete step-by-step solution -

We know that $A-B=A\bigcap {{B}^{c}}$
Hence we have $\left( A\bigcap B \right)\bigcup \left( A-B \right)=\left( A\bigcap B \right)\bigcup \left( A\bigcap {{B}^{c}} \right)$
Let $C=A\bigcap B$
We have
$\left( A\bigcap B \right)\bigcup \left( A-B \right)=C\bigcup \left( A\bigcap {{B}^{c}} \right)$
We know that union distributes over the intersection of two sets. Hence we have
$C\bigcup \left( A\bigcap {{B}^{c}} \right)=\left( C\bigcup A \right)\bigcap \left( C\bigcup {{B}^{c}} \right)$
Now $C\bigcup A=\left( A\bigcap B \right)\bigcup A$
We know that the union of two sets is associative, i.e. $A\bigcup B=B\bigcup A$
Hence we have
$C\bigcup A=A\bigcup \left( A\bigcap B \right)$
Using the distributive law of union over the intersection of two sets, we have
$C\bigcup A=\left( A\bigcup A \right)\bigcap (A\bigcup B)$
Now we know that $A\bigcup A=A$ (idempotent law).
Hence we have,
$C\bigcup A=A\bigcap \left( A\bigcup B \right)$
Since $A\subset A\bigcup B,\forall B\subset U$ and $A\bigcap B=A$ if $A\subset B$, we have
$C\bigcup A=A$
Also, $C\bigcup {{B}^{c}}=\left( A\bigcap B \right)\bigcup {{B}^{c}}$
Using commutative law of union of sets, we have
$C\bigcup {{B}^{c}}={{B}^{c}}\bigcup \left( A\bigcap B \right)$
Using the distributive law of union over the intersection of sets, we have
$C\bigcup {{B}^{c}}=\left( {{B}^{c}}\bigcup A \right)\bigcap \left( {{B}^{c}}\bigcup B \right)$
We know that ${{B}^{c}}\bigcup B=U$
Hence we have
$C\bigcup {{B}^{c}}=\left( {{B}^{c}}\bigcup A \right)\bigcap U$
Since ${{B}^{c}}\bigcup A\subset U$, we have
$C\bigcup {{B}^{c}}={{B}^{c}}\bigcup A$
Hence we have
$\left( A\bigcap B \right)\bigcup \left( A-B \right)=\left( C\bigcup A \right)\bigcap \left( C\bigcup {{B}^{c}} \right)=A\bigcap \left( {{B}^{c}}\bigcup A \right)$
We know that $A\subset A\bigcup B,\forall B\subset U$
Hence we have
$A\subset {{B}^{c}}\bigcup A$
Hence $\left( A\bigcap B \right)\bigcup \left( A-B \right)=A$
Q.E.D

Note: We can also verify the above result using Venn diagrams
Diagram for $A\bigcap B$:

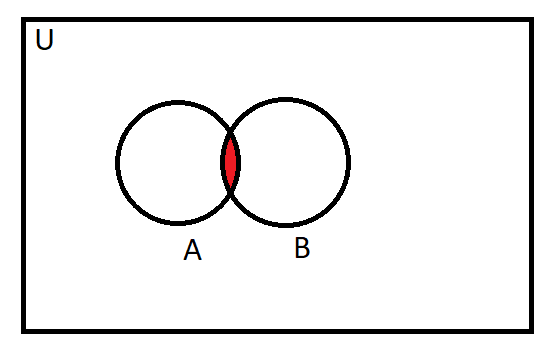
Diagram for A-B:

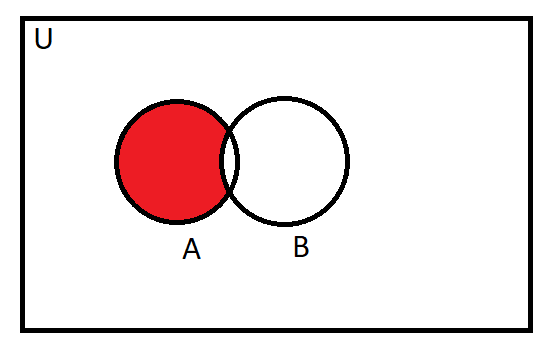
Diagram for $\left( A\bigcap B \right)\bigcup \left( A-B \right)$:

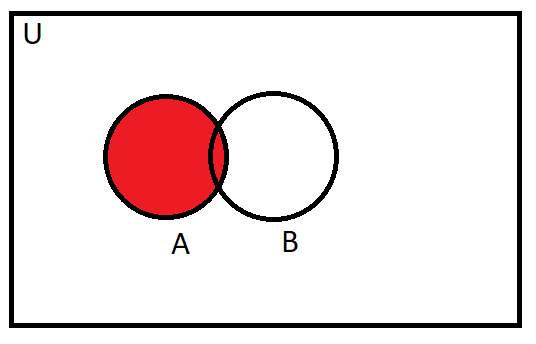
Hence $A=\left( A\bigcap B \right)\bigcup \left( A-B \right)$