Question

Prove that:
Chords equidistant from the centre of a circle are equal in length.

Answer 1

Hint: Let AB and CD are two chords of a circle with center O. Chord AB is at a distance of OM from the center of the circle and chord CD is at distance ON from the center of the circle. It is given that the chords are equidistant from the center of the circle, therefore, OM = ON.
Join OB and OC. Now, prove $\Delta BOM$ and $\Delta CON$ are congruent by the RHS rule of congruence and we get MB = NC. By using this relation, try to prove AB = CD

Complete step by step answer:
The given diagram shows the chords AB and CD at equidistant from the center of the circle O.
 

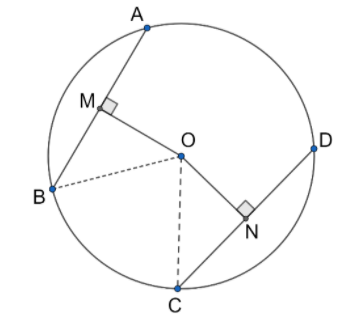
Join OB and OC.
We have $\Delta BOM$ and $\Delta CON$.
In $\Delta BOM$ and $\Delta CON$
OB = OC = radius of circle
OM = ON (given)
$\angle OMB=\angle ONC={{90}^{\circ }}$
So, by RHS rule of congruence,
\[~~\Delta BOM\cong \Delta CON\]
Since corresponding parts of congruent triangles are equal.
Therefore, \[MB=CN......(1)\]
Also, we know that the perpendicular from the center of a circle to a chord divides the chord into two equal halves.
Therefore, AM = MB and CN = ND
From equation (1) we have:
 \[MB=CN\]
Multiply both sides by 2, we get:
\[2MB=2CN\]
\[\Rightarrow MB+MB=CN+CN\]
Since AM = MB and CN = ND
We can write,
\[AM+MB=CN+ND\]
\[\Rightarrow AB=CD\]
Hence proved.

Therefore, chords equidistant from the center of a circle are equal in length.

Note: Instead of applying the RHS rule of congruence, we can apply Pythagoras theorem in both the triangles to prove AB = CD.
i.e.
OB = OC = radius of circle, say r
OM = ON = say d
So, by applying Pythagoras theorem in both the triangle, we get:
\[\begin{align}
  & MB=\sqrt{{{\left( OB \right)}^{2}}-{{\left( OM \right)}^{2}}} \\
 & =\sqrt{{{r}^{2}}-{{d}^{2}}}......(1)
\end{align}\]
\[\begin{align}
  & CN=\sqrt{{{\left( OC \right)}^{2}}-{{\left( ON \right)}^{2}}} \\
 & =\sqrt{{{r}^{2}}-{{d}^{2}}}......(2)
\end{align}\]
Hence, by comparing equation (1) and (2), we can say that MB = NC and therefore, AB = CD as proved earlier.