Question

Prove that any non-isosceles trapezium is not cyclic.

Answer 1

Hint: To show that the given non- isosceles trapezium is not cyclic. We have to keep in mind that for a quadrilateral to be a cyclic quadrilateral it's all the four vertices of a must inscribed in a circle must lie on the circumference of the circle. The measure of an exterior angle is equal to the measure of the opposite interior angle.

Complete step by step solution:
ABCD is non-isosceles trapezium. [Given].Let us consider a non-isosceles trapezium as ,

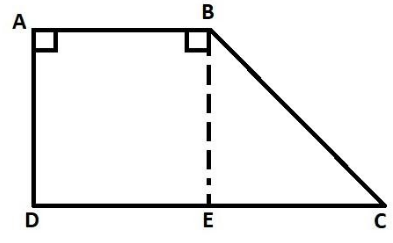
We have to prove that the given non-isosceles trapezium is not cyclic means that the given non-isosceles trapezium cannot be inscribed in the circle. We have to keep in mind that for a quadrilateral to be a cyclic quadrilateral it's all the four vertices of a must inscribed in a circle must lie on the circumference of the circle. The measure of an exterior angle is equal to the measure of the opposite interior angle.

In order to prove that this non-isosceles trapezium is not cyclic, we have to prove that the sum of opposite interior angle is not equal to ${180^\circ }$.Now,
$\angle D + \angle B$
$\angle D + \angle B = \angle D + \angle ABE + \angle CBE$
$\angle D + \angle B = {90^\circ } + {90^\circ } + \angle CBE$
$\angle D + \angle B = {180^\circ } + \angle CBE$
$\therefore \angle D + \angle B > {180^\circ }$
For a trapezium to be cyclic the sum of interior opposite angles must be supplementary , but here the sum of the angle ‘D’ and angle ‘B’ is greater than the ${180^ \circ }$ .

Hence ABCD is not cyclic.

Note: Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. In order to prove that this non-isosceles trapezium is not cyclic, we have to prove that the sum of opposite interior angles is not equal to ${180^\circ }$ .