Question

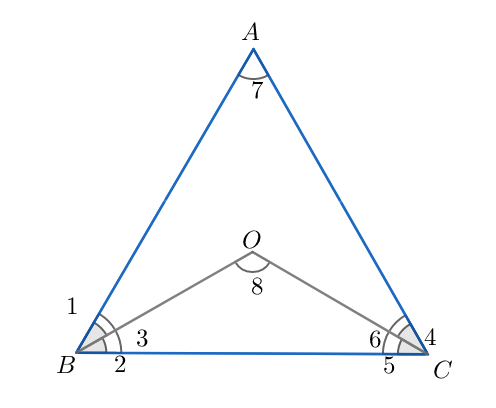
Prove that $\angle BOC=90+\dfrac{1}{2}\angle BAC$

Answer 1

Hint: Since this problem solely requires the concept of triangles and its various properties, we need to be well aware of them. Since this problem does not give any clear information about the angles and the relationship between them, we have to assume that OB and OC are the angle bisectors. After that, by applying the property of the sum of internal angles of a triangle, we can prove the desired equation.

Complete step by step solution:
The given problem is clearly a problem of geometry. This problem deals with the property of triangles such as its angle properties, the angle bisector properties and so on. Angle of a triangle refers to the angle held by the two sides of a triangle. Angle bisector means a line or a line segment which intersects two lines at a common point of intersection in such a manner that the angle held by the parent lines gets equally divided into two small angles.
In this problem, since all the angles are denoted by natural numbers, we will proceed with denoting the angles with natural numbers in our solution. By clear understanding, we can see that,
$\angle 3+\angle 6={{180}^{\circ }}-\angle 7....\left( i \right)$
Clearly, OB and OC are the angle bisectors of the angles $3$ and $6$ respectively. This means that angles $3$ and $6$ are divided equally into two equal angles by OB and OC. So, we can say that,
$\begin{align}
  & \angle 2=\dfrac{1}{2}\angle 3....\left( ii \right) \\
 & \angle 5=\dfrac{1}{2}\angle 6....\left( iii \right) \\
\end{align}$
Adding equations ii and iii, we get,
$\angle 2+\angle 5=\dfrac{1}{2}\angle 3+\dfrac{1}{2}\angle 6$
This can be further simplified to
$\angle 2+\angle 5=\dfrac{1}{2}\left( \angle 3+\angle 6 \right)$
Using equation i in the above equation, we get,
$\begin{align}
  & \Rightarrow \angle 2+\angle 5=\dfrac{1}{2}\left( {{180}^{\circ }}-\angle 7 \right) \\
 & \Rightarrow \angle 2+\angle 5={{90}^{\circ }}-\dfrac{1}{2}\angle 7....\left( iv \right) \\
\end{align}$
Now, using the property of sum of internal angles of a triangle, we get,
$\angle 8={{180}^{\circ }}-\left( \angle 2+\angle 5 \right)$
Using equation iv in the above equation, we get,
$\begin{align}
  & \angle 8={{180}^{\circ }}-\left( {{90}^{\circ }}-\dfrac{1}{2}\angle 7 \right) \\
 & \Rightarrow \angle 8={{90}^{\circ }}+\dfrac{1}{2}\angle 7 \\
\end{align}$
Therefore, we can conclude that $\angle BOC=90+\dfrac{1}{2}\angle BAC$ .

Note: It is to be noted that the given problem does not give any clear idea about the angles. So, we must assume something according to our need. But we must be careful not to assume anything limitlessly and this reduces the generosity of the problem.