Question

Prove that a triangle which has one of the angles as ${{30}^{\circ }}$ cannot have all vertices with integral coordinate.

Answer 1

Hint: In this question, we are given a triangle with one of the angles as ${{30}^{\circ }}$. We need to prove that all vertices cannot have integral coordinates. For this, we will first draw a triangle $\Delta ABC$ and make $\angle A$ as ${{30}^{\circ }}$ and mark coordinates of all three vertices. After that, we will find the slope of AB and AC. Then we will put values of angle $\theta $ and slope $\left( {{m}_{1}},{{m}_{2}} \right)$ in the formula $\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ for a triangle to prove our result. Slope of any line with end coordinate as $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is equal to $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ we will use $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$.

Complete step by step answer:
In this question, we are given a triangle with one of the angles as ${{30}^{\circ }}$. Let us suppose that triangle is $\Delta ABC$ with $\angle A$ equal to ${{30}^{\circ }}$. Let us suppose that the coordinate of A are $\left( {{x}_{1}},{{y}_{1}} \right)$ coordinates of B as $\left( {{x}_{2}},{{y}_{2}} \right)$ and the coordinate of C as $\left( {{x}_{3}},{{y}_{3}} \right)$.
Our figure looks like this,

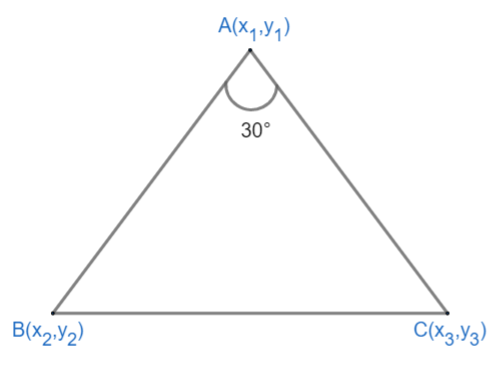
Now let us find the slope of the line AC and AB.
We know that the slope (m) of any line whose endpoints coordinate are $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
So, slope of line AB $\left( {{m}_{1}} \right)$ with end points having coordinate $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ will be given as,
${{m}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\cdots \cdots \cdots \left( 1 \right)$.
Similarly, slope of line AC $\left( {{m}_{2}} \right)$ with end point having coordinate $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{3}},{{y}_{3}} \right)$ will be given as,
${{m}_{2}}=\dfrac{{{y}_{3}}-{{y}_{1}}}{{{x}_{3}}-{{x}_{1}}}\cdots \cdots \cdots \left( 1 \right)$.
We know that, for a triangle having angle $\theta $ and corresponding scope of the side as ${{m}_{1}},{{m}_{2}}$ is given as $\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$.
So here for $\theta ={{30}^{\circ }}$. ${{m}_{1}},{{m}_{2}}$ as found earlier we have, $\tan {{30}^{\circ }}=\left| \dfrac{\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}-\dfrac{{{y}_{3}}-{{y}_{1}}}{{{x}_{3}}-{{x}_{1}}}}{1+\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( \dfrac{{{y}_{3}}-{{y}_{1}}}{{{x}_{3}}-{{x}_{1}}} \right)} \right|$.
Now taking LCM of $\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)$ in the denominator of both the numerator and denominator we get,
$\tan {{30}^{\circ }}=\left| \dfrac{\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)-\left( {{y}_{3}}-{{y}_{1}} \right)\left( {{x}_{2}}-{{x}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)}}{\dfrac{\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)+\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{y}_{3}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)}} \right|$.
Cancelling $\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)$ from the denominator of both the numerator and denominator we get,
$\tan {{30}^{\circ }}=\left| \dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)-\left( {{y}_{3}}-{{y}_{1}} \right)\left( {{x}_{2}}-{{x}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)+\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{y}_{3}}-{{y}_{1}} \right)} \right|$
We know that the value of $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ so we get,
$\dfrac{1}{\sqrt{3}}=\left| \dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)-\left( {{y}_{3}}-{{y}_{1}} \right)\left( {{x}_{2}}-{{x}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)+\left( {{y}_{2}}-{{y}_{1}} \right)\left( {{y}_{3}}-{{y}_{1}} \right)} \right|$
Now if we take the value of ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{y}_{1}},{{y}_{2}},{{y}_{3}}$ all are integers then the right hand side of the equation will become a rational number of the form $\dfrac{p}{q}\left( q\ne 0 \right)$ because multiplication, addition, subtraction of integers gives us integer.
But the left side of the equation is irrational ($\sqrt{3}$ is an irrational number). So the right side cannot be rational. So all the coordinate cannot be integers.
Hence a triangle which has one of the angles as ${{30}^{\circ }}$ cannot have all vertices with integral coordinate.

Note: Students should take care of the signs while solving this sum. Make sure to take the slope of only those sides which are adjacent to the given angle. Students should know the formula of the slope and $\tan \theta $ for solving this sum.