Question

Prove that a line drawn through the midpoint of one side of a triangle parallel to another side bisects the third side.

Answer 1

Hint: We first draw the given conditions and find a line through C parallel to BA. Then we prove that FBCG is a parallelogram using its parallel lines. Then we find congruence between $\Delta AFE$ and $\Delta ECG$ with the help of AAS. We prove that $AE=EC$ for CPCT of congruency.

Complete step by step answer:
Let’s assume for the $\Delta ABC$, we are drawing a line through the midpoint F of side AB parallel to another side BC. So, $AF=FB$. The line intersects side AC at E.

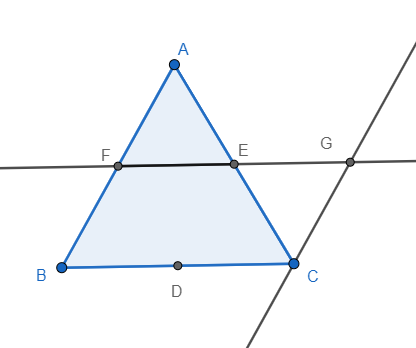
We have to show point E bisects the side AC which means $AE=EC$.
Step: 1
We first draw a line through C parallel to BA which intersects the extended FE at point G.
We got $AB||GC$. Also, we have $FE||BC$ which means $FG||BC$.
Step: 2
For quadrilateral FBCG, we have $FG||BC$ and $FB||GC$. So, FBCG is parallelogram has opposite sides are parallel. So, $AF=FB=GC$.
Step: 3
In between $\Delta AFE$ and $\Delta ECG$,
(i) $\angle FEA=\angle CEG[opposite]$
(ii) $\angle FAE=\angle ECG[alternate]$
(iii) $AF=GC$
So, $\Delta AFE\cong \Delta ECG[A-A-S]$
We get from C.P.C.T that $AE=EC$.
Thus proved.

Note: We need to remember that it also gives us $FE=EG$ from CPCT. We have $FG=BC$ from the parallelogram FBCG. So, $FE=EG=\dfrac{1}{2}FG=\dfrac{1}{2}BC$. This theorem also proves that the parallel line is half of the opposite side.