
How do you prove $\tan ( - a) = \tan ({360^o} - a) = - \tan (a)$ ?
Answer
542.1k+ views
Hint: In a unit circle, when we move anti-clockwise we get a positive angle and when we move clockwise we get a negative angle. Tangent or $\tan $ of an angle $\theta $ is given by $\tan \theta = \dfrac{{perpendicular}}{{base}}$ which in terms of trigonometric ratios we can write as $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$. We will observe the unit circle for values and signs of $\tan $ in various quadrants to arrive at the conclusion.
Complete step by step answer:
To understand the behavior of $\tan $ for negative angles we draw a unit circle.
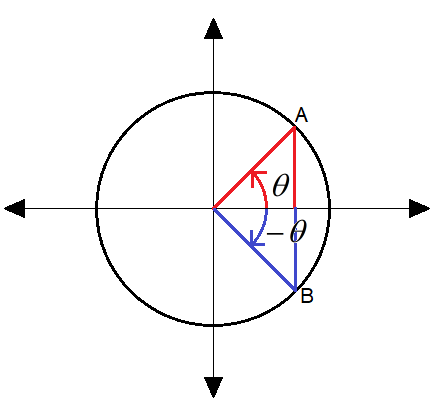
We can see from above diagram that,
For point B, from clockwise we can write the angle as $ - \theta $, but from anti-clockwise we can write the same angle as $({360^o} - \theta )$. The value and sign of $\tan $of both angles $ - \theta $ and $({360^o} - \theta )$ would be same as we are dealing with the same angles, i.e. we can write,
$\tan ( - \theta ) = \tan ({360^o} - \theta )$
Further,
for point A in quadrant 1 with angle $\theta $, $\tan \theta $ is positive as both perpendicular and base is positive,
and for point B in the quadrant 4 with angle $ - \theta $ from clockwise, $\tan ( - \theta )$ is negative as base is positive but perpendicular is negative.
We can make a table with further observation:
Thus, we see from the above table that the sign of $\tan ( - \theta )$ is always opposite to that of $\tan \theta $. But the value will be the same as the value of perpendicular and base would be the same.
So we can write,
$\tan ( - \theta ) = \tan \theta $ but with opposite sign, or
$\tan ( - \theta ) = - \tan \theta $
Thus, we get $\tan ( - \theta ) = \tan ({360^o} - \theta )$ and $\tan ( - \theta ) = - \tan \theta $.
Hence, for any angle $a$ we can write $\tan ( - a) = \tan ({360^o} - a) = - \tan (a)$.
Note: The sign of the perpendicular and base is positive or negative depending on the side of axis it lies on. The value of $\tan \theta $ and $\tan ( - \theta )$ is the same, only the sign is opposite, i.e. when $\tan \theta $ is positive $\tan ( - \theta )$ is negative, and vice-versa. As we wrote $ - \theta $ as $({360^o} - \theta )$ from anti-clockwise, we can also write $\theta $ as $ - ({360^o} - \theta )$ from clockwise direction. We will get $\tan \theta = \tan ( - ({360^o} - \theta )) = \tan (\theta - {360^o})$.
Complete step by step answer:
To understand the behavior of $\tan $ for negative angles we draw a unit circle.

We can see from above diagram that,
For point B, from clockwise we can write the angle as $ - \theta $, but from anti-clockwise we can write the same angle as $({360^o} - \theta )$. The value and sign of $\tan $of both angles $ - \theta $ and $({360^o} - \theta )$ would be same as we are dealing with the same angles, i.e. we can write,
$\tan ( - \theta ) = \tan ({360^o} - \theta )$
Further,
for point A in quadrant 1 with angle $\theta $, $\tan \theta $ is positive as both perpendicular and base is positive,
and for point B in the quadrant 4 with angle $ - \theta $ from clockwise, $\tan ( - \theta )$ is negative as base is positive but perpendicular is negative.
We can make a table with further observation:
| When $\theta $ lies in quadrant 1 | $ - \theta $ lies in quadrant 4 | $\tan \theta $ is positive | $\tan ( - \theta )$is negative |
| When $\theta $ lies in quadrant 2 | $ - \theta $ lies in quadrant 3 | $\tan \theta $ is negative | $\tan ( - \theta )$is positive |
| When $\theta $ lies in quadrant 3 | $ - \theta $ lies in quadrant 2 | $\tan \theta $ is positive | $\tan ( - \theta )$is negative |
| When $\theta $ lies in quadrant 4 | $ - \theta $ lies in quadrant 1 | $\tan \theta $ is negative | $\tan ( - \theta )$is positive |
Thus, we see from the above table that the sign of $\tan ( - \theta )$ is always opposite to that of $\tan \theta $. But the value will be the same as the value of perpendicular and base would be the same.
So we can write,
$\tan ( - \theta ) = \tan \theta $ but with opposite sign, or
$\tan ( - \theta ) = - \tan \theta $
Thus, we get $\tan ( - \theta ) = \tan ({360^o} - \theta )$ and $\tan ( - \theta ) = - \tan \theta $.
Hence, for any angle $a$ we can write $\tan ( - a) = \tan ({360^o} - a) = - \tan (a)$.
Note: The sign of the perpendicular and base is positive or negative depending on the side of axis it lies on. The value of $\tan \theta $ and $\tan ( - \theta )$ is the same, only the sign is opposite, i.e. when $\tan \theta $ is positive $\tan ( - \theta )$ is negative, and vice-versa. As we wrote $ - \theta $ as $({360^o} - \theta )$ from anti-clockwise, we can also write $\theta $ as $ - ({360^o} - \theta )$ from clockwise direction. We will get $\tan \theta = \tan ( - ({360^o} - \theta )) = \tan (\theta - {360^o})$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




