Question

Prove: $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = 1.

Answer 1

Hint: By definition, in a right−angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
sin θ = $ \dfrac{P}{H} $ , cos θ = $ \dfrac{B}{H} $ , tan θ = $ \dfrac{P}{B} $ .
Recall that the Pythagoras' theorem holds true for every right−angled triangle: $ {{P}^{2}} $ + $ {{B}^{2}} $ = $ {{H}^{2}} $ . If we assume one of the non−right−angles as θ and write an expression in terms of P, B and H for sin θ and cos θ using the definition above, we will get the result.

Complete step-by-step answer:
Let's say we have a right−angled triangle with the side opposite to the angle θ as P (perpendicular) and H as the hypotenuse. The third side, adjacent to the angle, call it B (base).
It can be represented as follows:

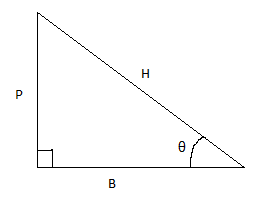
By definition, sin θ = $ \dfrac{Perpendicular}{Hypotenuse} $ = $ \dfrac{P}{H} $ and cos θ = $ \dfrac{Base}{Hypotenuse} $ = $ \dfrac{B}{H} $ .
Therefore, $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = $ {{\left( \dfrac{P}{H} \right)}^{2}} $ + $ {{\left( \dfrac{B}{H} \right)}^{2}} $ .
⇒ $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = $ \dfrac{{{P}^{2}}}{{{H}^{2}}} $ + $ \dfrac{{{B}^{2}}}{{{H}^{2}}} $
⇒ $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = $ \dfrac{{{P}^{2}}+{{B}^{2}}}{{{H}^{2}}} $
We know that, because of the Pythagoras' theorem, $ {{P}^{2}} $ + $ {{B}^{2}} $ = $ {{H}^{2}} $ . By substituting this in the above expression, we will get:
⇒ $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = $ \dfrac{{{H}^{2}}}{{{H}^{2}}} $
⇒ $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = 1. Hence, proved.
Note: There are many ways to prove the Pythagoras' theorem. For instance, it can be proved by using the properties of similar triangles, by drawing a perpendicular on the hypotenuse from the right−angled vertex and observing that the two smaller triangles have the same values of the angles and are thus similar.
Since $ {{\sin }^{2}}\theta $ + $ {{\cos }^{2}}\theta $ = 1, we can divide both sides by $ {{\cos }^{2}}\theta $ or $ {{\sin }^{2}}\theta $ to get $ {{\tan }^{2}}\theta $ + 1 = $ {{\sec }^{2}}\theta $ and 1 + $ {{\cot }^{2}}\theta $ = $ {{\csc }^{2}}\theta $ respectively.
It can also be observed from the right angled−triangle, that sin (90˚ − θ) = cos θ etc.