Question

How do you prove \[{\sec ^{ - 1}}x + \cos e{c^{ - 1}}x = \dfrac{\pi }{2}\] ?

Answer 1

Hint: These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios. So, we will substitute and solve accordingly. By using the Pythagoras theorem, we know \[\sin \theta = \dfrac{{Opposite}}{{Hypotenuse}}\] . We will use this identity \[si{n^{-1}}a + si{n^{-1}}b = si{n^{-1}}(a\sqrt {1-{b^2}} + b\sqrt {1-{a^2}} )\] and solve this given equation and get the final output.

Complete step-by-step answer:
Inverse function: If y=f(x) and x=g(y) are two functions such that f(g(y))=y and g(f(y))=x, then f and y are said to be inverse of each other \[x = {f^{ - 1}}(y)\].
As we know that trigonometric functions are not one-one and onto in their natural domain and range, so their inverse do not exist but if we restrict their domain and range, then their inverse may exist.
Given that,
\[{\sec ^{ - 1}}x + \cos e{c^{ - 1}}x = \dfrac{\pi }{2}\]
Let,
\[{\sec ^{ - 1}}x = y\]
\[ \Rightarrow x = \sec y\]
\[ \Rightarrow x = \cos ec\left( {\dfrac{\pi }{2} - y} \right)\]
\[ \Rightarrow \cos e{c^{ - 1}}x = \dfrac{\pi }{2} - y\]
Substituting back the value of y, we will get,
\[ \Rightarrow \cos e{c^{ - 1}}x = \dfrac{\pi }{2} - {\sec ^{ - 1}}x\]
By using transposing method, move the RHS term to LHS term, we will get,
\[ \Rightarrow \cos e{c^{ - 1}}x + {\sec ^{ - 1}}x = \dfrac{\pi }{2}\]
Rearrange this, we will get,
\[ \Rightarrow {\sec ^{ - 1}}x + \cos e{c^{ - 1}}x = \dfrac{\pi }{2}\]

Note: Let,
\[{\sec ^{ - 1}}x = \theta \]
\[ \Rightarrow x = \sec \theta \]
\[ \Rightarrow x = \dfrac{1}{{\cos \theta }}\]
\[ \Rightarrow \cos \theta = \dfrac{1}{x}\]
\[ \Rightarrow \dfrac{1}{x} = \cos \theta \]
\[ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{x}} \right)\]
\[ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{x}} \right)\]
According to the Pythagoras theorem, we will draw the diagram as below:

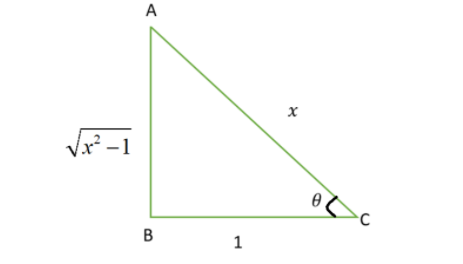
We know that, \[\sin \theta = \dfrac{{Opposite}}{{Hypotenuse}} = \dfrac{{AB}}{{AC}}\]
\[\sin \theta = \dfrac{{\sqrt {{x^2} - 1} }}{x}\]
\[ \Rightarrow \theta = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{x^2} - 1} }}{x}} \right)\]
Now,
\[\therefore {\sec ^{ - 1}}x + \cos e{c^{ - 1}}x\]
\[ = {\cos ^{ - 1}}\left( {\dfrac{1}{x}} \right) + {\sin ^{ - 1}}\left( {\dfrac{1}{x}} \right)\]
\[ = \theta + {\sin ^{ - 1}}\left( {\dfrac{1}{x}} \right)\]
Substituting the value of \[\theta \] , we will get,
\[ = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{x^2} - 1} }}{x}} \right) + {\sin ^{ - 1}}\left( {\dfrac{1}{x}} \right)\]
We know the identity \[si{n^{-1}}a + si{n^{-1}}b = si{n^{-1}}(a\sqrt {1-{b^2}} + b\sqrt {1-{a^2}} )\] , and so applying this, we will get,
\[ = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{x^2} - 1} }}{x} \times \sqrt {1 - \dfrac{1}{{{x^2}}}} + \sqrt {1 - \dfrac{{{x^2} - 1}}{{{x^2}}}} \times \dfrac{1}{x}} \right)\]
\[ = {\sin ^{ - 1}}\left( {\dfrac{{\sqrt {{x^2} - 1} }}{x} \times \dfrac{{\sqrt {{x^2} - 1} }}{x} + \dfrac{1}{x} \times \dfrac{1}{x}} \right)\]
\[ = {\sin ^{ - 1}}\left( {\dfrac{{{x^2} - 1}}{{{x^2}}} + \dfrac{1}{{{x^2}}}} \right)\]
Taking LCM, we will get,
\[ = {\sin ^{ - 1}}\left( {\dfrac{{{x^2} - 1 + 1}}{{{x^2}}}} \right)\]
\[ = {\sin ^{ - 1}}\left( 1 \right)\]
\[ = \dfrac{\pi }{2}\]
Hence, it is proved that \[{\sec ^{ - 1}}x + \cos e{c^{ - 1}}x = \dfrac{\pi }{2}\] .