Question

Prove geometrically that:
\[\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B\]

Answer 1

Hint:
Here we have to prove the given trigonometric identity. For that, we will first draw triangles and we will apply the basic trigonometric formulas using each triangle. Then we will find the relation between the sides of each triangle and simplify the terms further to prove \[\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B\].

Complete step by step solution:
We will first draw three triangles like that:-

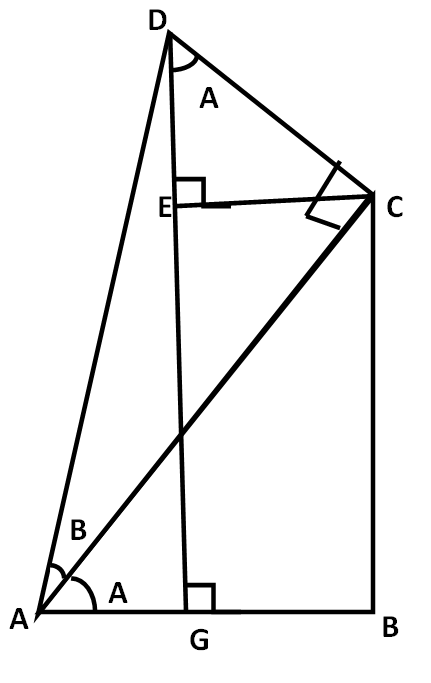
In the above figure,
\[EC\] is parallel to \[AB\]
\[\angle CAB\] and \[\angle ACE\] are alternate angles.
Therefore,
\[\angle CAB = \angle ACE = \angle A\]
We know from the figure,
\[ \Rightarrow \angle ACD = \angle ACE + \angle DCE = {90^ \circ }\]
After substituting the value, we get
\[\begin{array}{l} \Rightarrow A + \angle DCE = {90^ \circ }\\ \Rightarrow \angle DCE = {90^ \circ } - A\end{array}\]
We know from the properties of triangles that the sum of all angles of a triangle is \[{180^ \circ }\].
Applying this property in $\Delta DCE$, we get
\[ \Rightarrow \angle DCE + \angle DEC + \angle EDC = {180^ \circ }\]
Now, we will substitute the value of angles here.
\[\begin{array}{l} \Rightarrow 90^\circ - A + 90^\circ + \angle EDC = 180^\circ \\ \Rightarrow \angle EDC = A\end{array}\]
Applying trigonometric formulas in triangle \[ACB\], we get
\[\cos A = \dfrac{{AB}}{{AC}}\]
Applying trigonometric formulas in triangle \[ACD\], we get
\[\begin{array}{l}\sin B = \dfrac{{CD}}{{AD}}\\\cos B = \dfrac{{AC}}{{AD}}\end{array}\]
In triangle \[ADG\],
\[\angle DAG = \angle DAC + \angle CAB\]
Substituting all the values here, we get
\[\angle DAG = \angle B + \angle A\]
Applying trigonometric formulas in triangle \[AGD\], we get
 \[\cos \left( {A + B} \right) = \dfrac{{AG}}{{AD}}\] …….. \[\left( 1 \right)\]
We can write \[DG\] as the sum of \[BG\] and \[AB\].
Now, we will substitute these values in equation \[\left( 1 \right)\].
\[\begin{array}{l} \Rightarrow \cos \left( {A + B} \right) = \dfrac{{AB + GB}}{{AD}}\\ \Rightarrow \cos \left( {A + B} \right) = \dfrac{{AB}}{{AD}} + \dfrac{{GB}}{{AD}}\end{array}\]
Now, we will multiply the denominator and numerator of the first fraction by \[AC\] and we will multiply the denominator and numerator of the first fraction by \[DC\].
\[ \Rightarrow \cos \left( {A + B} \right) = \dfrac{{AB}}{{AC}} \times \dfrac{{AC}}{{AD}} + \dfrac{{GB}}{{DC}} \times \dfrac{{DC}}{{AD}}\]
Substituting the calculated values here, we get
\[ \Rightarrow \cos \left( {A + B} \right) = \cos A \times \cos B + \dfrac{{GB}}{{DC}} \times \sin B\]
As \[GB = EC\], therefore,
\[ \Rightarrow \cos \left( {A + B} \right) = \cos A \times \cos B + \dfrac{{EC}}{{DC}} \times \sin B\]
Now, we will substitute the value of \[\dfrac{{EC}}{{DC}}\] here.
\[ \Rightarrow \cos \left( {A + B} \right) = \cos A \times \cos B + \sin A \times \sin B\]

Hence, we have proved the given trigonometric identity.

Note:
We need to know the meaning of the trigonometric identities as we have used the trigonometric identities in this question. Trigonometric identities are defined as the equalities which involve the trigonometric functions and they are true for every value of the occurring variables for which both sides of the equality are defined. We need to keep in mind that all the trigonometric identities are periodic in nature. They repeat their values after a certain interval.