Question

Prove geometrically that:
 $ \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B $

Answer 1

Hint: In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
 $ \sin \theta =\dfrac{P}{H},\cos \theta =\dfrac{B}{H},\tan \theta =\dfrac{P}{B} $
 $ {{P}^{2}}+{{B}^{2}}={{H}^{2}} $ (Pythagoras' Theorem)
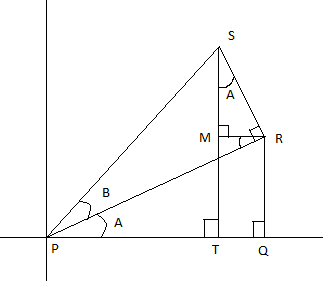
Draw a right-angled $ \Delta PQR $ with $ \angle Q={{90}^{\circ }} $ and $ \angle P=A $ . At the point P, draw another right-angled triangle $ \Delta PRS $ on the hypotenuse of $ \Delta PQR $ , such that $ \angle R={{90}^{\circ }} $ and $ \angle P=B $ . Finally, drop a line ST perpendicular on PQ to complete a right-angled triangle $ \Delta PTS $ with $ \angle T={{90}^{\circ }} $ and $ \angle P=A+B $ , and complete the proof by considering the lengths of the sides of the triangles. Also draw $ RM\bot ST $ .

Complete step-by-step answer:
To prove: $ \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B $ .

Proof: Using the definition of trigonometric ratios:
In $ \Delta PQR $ :
 $ \cos A=\dfrac{PQ}{PR} $ ... (1).
In $ \Delta PRS $ :
 $ \cos B=\dfrac{PR}{PS} $ ... (2).
 $ \sin B=\dfrac{SR}{PS} $ ... (3).
Since $ MR\parallel PQ $ , $ \angle MRP=\angle PRQ=A $ (Alternate interior angles), and so $ \angle MRS={{90}^{\circ }}-A $ .
∴ In $ \Delta SMR $ , $ \angle MSR={{90}^{\circ }}-({{90}^{\circ }}-A)=A $ , and:
 $ \sin A=\dfrac{RM}{SR} $ ... (4).
Now, using equations (1) and (2), we get:
 $ \cos A.\cos B=\dfrac{PQ}{PR}.\dfrac{PR}{PS}=\dfrac{PQ}{PS} $ ... (5).
Finally, in $ \Delta PTS $ :
 $ \cos (A+B)=\dfrac{PT}{PS}=\dfrac{PQ-QT}{PS} $
Since QT = MR, we can write:
 $ \cos (A+B)=\dfrac{PQ}{PS}-\dfrac{RM}{PS} $
⇒ $ \cos (A+B)=\dfrac{PQ}{PS}-\dfrac{RM}{SR}.\dfrac{SR}{PS} $
Using equations (3), (4) and (5):
 $ \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B $

Note: Using the fact that $ \cos (-\theta )=\cos \theta $ and $ \sin (-\theta )=-\sin \theta $ , we will get:
 $ \cos \left( A-B \right)=\cos A\cos B+\sin A\sin B $
Similar strategy can be applied to prove results for $ \sin (A\pm B) $ .
There are many other ways to prove the result: using a unit circle, other types of constructions, etc.