Question

How do you prove corresponding angles are equal?

Answer 1

Hint: First, draw two parallel lines and a transverse intersecting them and name all the points. Then observe and find the pairs of corresponding angles present in the diagram. Recall the other properties like alternate exterior angle property and vertically opposite angle property and relate them to each other to prove one pair of corresponding angles equal.

Complete step-by-step answer:

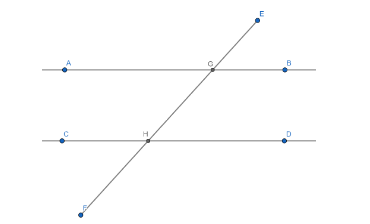
(i)
As we know that, corresponding angles are any pair of angles each of which is on the same side of one of two parallel lines cut by a transversal and on the same side of transversal.
Here, the pairs of corresponding angles are:
 $ \angle AGE $ and $ \angle CHG $
 $ \angle AGH $ and $ \angle CHF $
 $ \angle BGE $ and $ \angle DHG $
 $ \angle BGH $ and $ \angle DHF $
We have to prove one of these pairs equal. So,
To prove: $ \angle AGE = \angle CHG $
(ii)
As we know that line segment $ AB $ is parallel to the line segment $ CD $ i.e., $ AB||CD $ . We also know that the pair of angles which lie on the outer side of the two parallel lines but on either side of the transversal line are equal and are called alternate exterior angles.
So, by alternate exterior angle property,
 $ \angle AGE = \angle DHF $
(iii)
We also know that the angles opposite to each other when two lines intersect are equal to each other and are called vertically opposite angle.
So, by vertically opposite angle property,
 $ \angle DHF = \angle CHG $
(iv)
As we know that, for any numbers $ a,b,c $ if $ a = b $ and $ b = c $ then $ a = c $ . This property is called the transitive property of equality.
Since we get,
 $ \angle AGE = \angle DHF $
And, $ \angle DHF = \angle CHG $
So, by transitive property of equality, we get:
 $ \angle AGE = \angle CHG $
Hence, proved.

Note: We could also prove this question by using alternate interior angle property to prove $ \angle AGH = \angle DHG $ as they are in the interior side and on the either side of the transversal line and then subtracting both of these angles from $ 180^\circ $ to obtain $ \angle AGE $ on LHS and $ \angle CHG $ on the RHS by supplementary angles property.