Question

Projectile is projected at an angle ($\alpha$>45°) with an initial velocity u. The time t, at which its magnitude of horizontal velocity will be equal the magnitude of vertical velocity is :-
(1) $t=\dfrac{u}{g}(\cos \alpha -\sin \alpha )$
(2) $t=\dfrac{u}{g}(\cos \alpha +\sin \alpha )$
(3) $t=\dfrac{u}{g}(\sin \alpha -\cos \alpha )$
(4) $t=\dfrac{u}{g}({{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha )$

Answer 1

Hint: From the projectile projected at an angle ($\alpha \rangle {{45}^{0}}$) with an initial velocity u, first find the expression for vertical velocity component and then the horizontal velocity component. Then equate both the velocity equal and find the value of time in the equation.

Complete step by step answer:
The figure below shows projectile motion, object projected at an angle $\alpha$, where $\alpha \rangle {{45}^{0}}$, and ${{v}_{x}},{{v}_{y}}$ and v are x-component of velocity, y-component of velocity and velocity respectively.

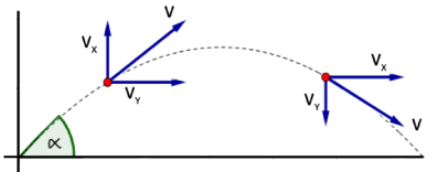
The formula for horizontal or x-component of velocity is,
${{v}_{x}}=u\cos (\alpha )$ ….(i)
Where, u is initial velocity of projectile and $\alpha$is angle of projection.

The formula for vertical or y-component of velocity is,
${{v}_{y}}=u\sin (\alpha )-gt$ ….(ii)
Where, u is initial velocity of projectile, $\alpha$is angle of projection and g is acceleration due to gravity and time t is time of projectile motion.

Now to calculate the time t, at which magnitude of horizontal velocity will be equal the magnitude of vertical velocity we equate equation(i) and equation(ii) we get,
$u\cos (\alpha )=u\sin (\alpha )-gt$
$\Rightarrow gt=u\sin (\alpha )-u\cos (\alpha )$
$\Rightarrow gt=u[\sin (\alpha )-\cos (\alpha )]$
$\Rightarrow t=\dfrac{u[\sin (\alpha )-\cos (\alpha )]}{g}$

Hence, the correct answer is option (3).

Additional Information:
The horizontal or x-component of velocity and vertical or y-component of velocity of an object in projectile motion are independent of each other. There is acceleration only in vertical direction and not in horizontal direction i.e. the velocity in horizontal direction is constant equal to g, the acceleration due to gravity (free fall).

Note:
It is important for students to memorize the formulae of horizontal or x-component of velocity and vertical or y-component of velocity of an object in projectile motion, also it is easier if one remembers the formula of time of projectile motion, to solve such questions quickly.