Question

Prepare a model
 (a) for Inequalities of a triangle
(b)for Pythagoras theorem
(c)To find distance without tape
(d)To show Tangent is always perpendicular to the radius of the circle
(e)To show “angles in same segment of a circle are equal.”
(f)To find Area of a circle

Answer 1

Hint:We use the construction on graph paper for a model of Pythagoras theorem(we draw squares), to show tangent is always perpendicular to the radius of the circle (circle and lines), to show “angles in the same segment of a circle are equal” and to find an area of a circle. We draw shift the vertex of an isosceles triangle to check inequality and take chalk as a unit to measure distance without tape.

 Complete step by step answer:

(a) for Inequalities of a triangle
We take the ruler and draw a line segment BC. Then we find the middle point of the segment with compass and draw the perpendicular bisector . We take a point A and draw a line perpendicular to BC . We obtain isosceles triangle ABC where AB=AC and $\angle ABC=\angle ACB.$ We take different points D on left side of A and E on the right side of A. We join D,E with B and C .

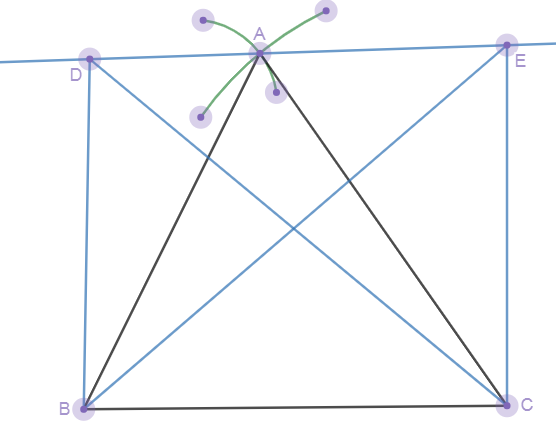
We observe that while in triangle ABC we have AB=AC because but when we move to D from A we have $\angle DBC > DCB$ and we measure their respective opposite sides to get $CD > BD$. Summarily if we move from A to E we have $\angle EBC < \angle ECB$ and we measure their respective opposite sides to get $EB > EC$. So we got the model for inequalities for a triangle to show the greater angle will have greater side opposite to it.


(b) for Pythagoras theorem: Let us assume the lengths of the right-angled triangle be where is the hypotenuse we construct a square ABCD on graph paper as shown below with E, F, G, H as the midpoints of AB,BC,CD,AD respectively. We join EFGH.

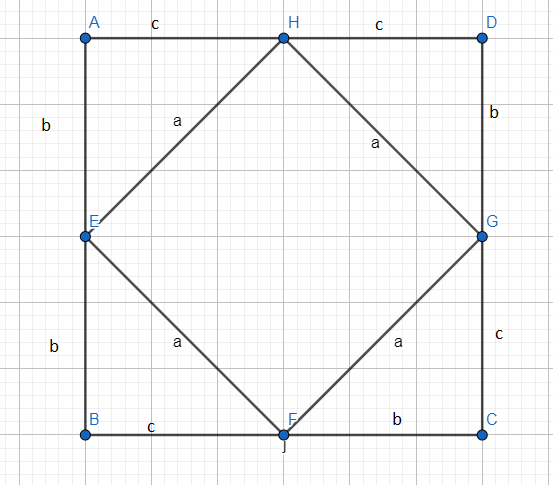
We find the area of the squares ABCD , EFGH and the triangles AEF, EBF, FCG, DGH by counting the unit square centimetres and millimetres. We find the areas of the triangles AEF, EBF, FCG, DGH and get as equal. We see that area of ABCD is the sum of areas of the square EFGH and 4 time the area of the triangle AEH. So we have,
\[\begin{align}
  & {{\left( b+c \right)}^{2}}={{a}^{2}}+4\times \dfrac{1}{2}\times bc \\
 & \Rightarrow {{b}^{2}}+{{c}^{2}}={{a}^{2}} \\
\end{align}\]
 So we have the model for Pythagoras theorem.

(c)To find distance without tape: We take a piece of chalk for the model of unit distance. We then measure the length of any object as a integral multiple or fractional part of the chalk.
(d)To show Tangent is always perpendicular to the radius of the circle. We draw any circle and then draw a diameter by joining any two points. We draw lines parallel to the diameter until one line touches the circle. We join the point of contact with the centre and measure the angle the radius subtends. We find it to be right-angled.

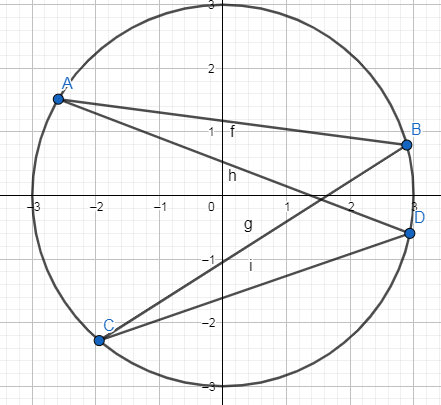
(e)To show “angles in same segment of a circle are equal.” We draw a circle on the graph paper ad take a segment AC we subtend two angle in the circle ABC and ADC and we measure them with a protractor. We have $\angle ABC=\angle ADC$

(f)To find Area of a circle
We draw any circle on graph paper and count the squares with length 1cm and 1mm to find the area. We verify it with the formula for area $A=\pi {{r}^{2}}$

Note:
 We can also use nails to demonstrate points and soldering balls to cover a particular region to measure area. The number of balls that can be placed within the region will be analogues to its area.