Question

Pravali house has a water tank in the shape of a cylinder on the roof .this is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid .The sump has dimensions \[1.57m\times 1.44m\times 1.5m\] .The water tank has radius 60cm and a height of 95 cm. Find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Compare the capacity of the tank with that of the sump.(use $\pi =3.14$ )

Answer 1

Hint: To find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water, we have to find the volume of cylinder and cuboid using the formula $\pi {{r}^{2}}h$ and \[lbh\] respectively. Then subtract the volume of the cylinder from that of the cuboid to get the volume of water left in the sump. Use this result and formula \[lbh\] with the same length and breadth to find the height, h of the water left in the sump. Now, to compare the capacity of the tank with that of the sump, we will divide the volume of the cylinder by the volume of the cuboid.

Complete step by step answer:
We have to find the height of the water left in the sump after the water tank has been completely filled with water from the sump which had been full of water. Also, we have compared the capacity of the tank with that of the sump.

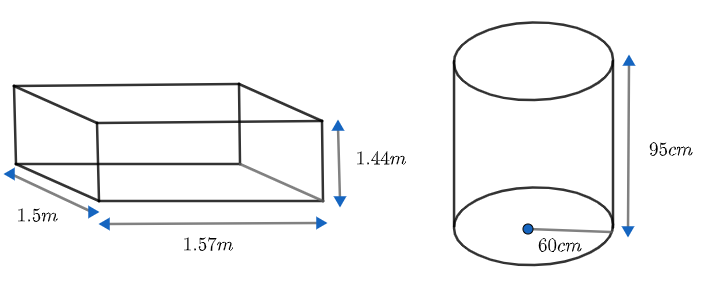
We have,
Height of the cylindrical tank, $h=95cm$
Let’s convert it into meters. We will get
$h=\dfrac{95}{100}m=0.95m$
We also have, radius of the tank, $r=60cm$
Let’s convert it into meters. We will get
$h=\dfrac{60}{100}m=\dfrac{3}{5}m$
Now, we have to find the volume of the cylinder.
We know that volume of a cylinder $=\pi {{r}^{2}}h$
Let us substitute the values in the above formula. We will get
Volume of a cylinder $=3.14\times {{\left( \dfrac{3}{5} \right)}^{2}}\times 0.95$
We can write this as
Volume of a cylinder $=3.14\times \dfrac{9}{25}\times 0.95$
On multiplication, we will get
Volume of a cylinder $=\dfrac{26.847}{25}$
On division, we will get
Volume of a cylinder $=1.073{{m}^{3}}...(i)$
We have the length, breadth and height of the cuboid as \[1.57m\times 1.44m\times 1.5m\] .
Let’s find the volume of the cuboid which is given by $\text{length}\times \text{breadth}\times \text{height}$ .
\[\Rightarrow \text{Volume of the cuboid}=lbh\]
Let us substitute the values in the above formula. We will get
Volume of the cuboid \[=1.57\times 1.44\times 1.5\]
On multiplication, we will get
Volume of the cuboid \[=3.391{{m}^{3}}...(ii)\]
Let’s find the volume of water left in the sump. This is done by subtracting (i) from (ii).
\[\Rightarrow \text{Volume of water left in the sump}=3.391-1.073=2.318{{m}^{3}}\]
We know that \[\text{Volume of the cuboid}=lbh\] . Hence,
\[lbh=2.318{{m}^{3}}\]
The length and breadth will be the same. Only the height of water changes. Hence, we can find h as
\[\Rightarrow 2.26\times h=2.318\]
Let us take 2.26 to the LHS. We will get
\[\begin{align}
  & h=\dfrac{2.318}{2.26} \\
 & \Rightarrow h=1.025m \\
\end{align}\]
Let us first compare the capacity of the tank with that of the sump, that is, their volume. This is done by taking their ratio.
$\dfrac{\text{Volume of cylinder}}{\text{Volume of a cuboid}}=\dfrac{1.073}{3.391}$
On solving this, we will get
$\dfrac{\text{Volume of cylinder}}{\text{Volume of a cuboid}}=0.31$
We can write 0.31 approximately as 0.3. That is,
$\dfrac{\text{Volume of cylinder}}{\text{Volume of a cuboid}}=\dfrac{3}{10}$

Hence, the capacity of the tank is $\dfrac{3}{10}$ times the capacity of the sump.

Note: You must convert all the units to a single one before solving. You may make errors when writing the formula for volume of cylinder as $2\pi rh$ . Also, there can be an error when writing the volume of cuboid as $2\left( l+w \right)h$ . Be careful when finding the ratio. Do not divide the capacity of the cuboid by the capacity of the cylinder.