Question

PQT and PR are tangents to the circle. If $$\mathrm{\angle }QPR={38}^{\circ }$$, $$\mathrm{\angle }PRS={111}^{\circ }$$. Find $$\mathrm{\angle }TQS$$.

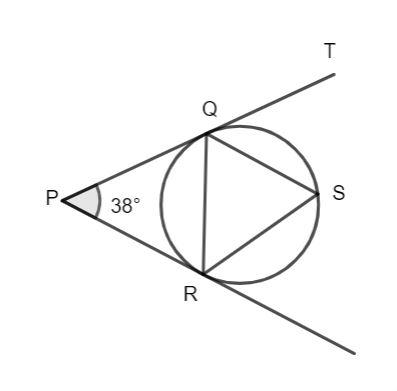
Answer 1

Hint: Find the angles PRQ and PQR using the properties of a tangent to the circle. Then find the angle RSQ, using the properties of the angle subtended by the chord. Then find angle RQS using properties of the triangle and finally find the angle TQS.

Complete Step-by-Step solution:

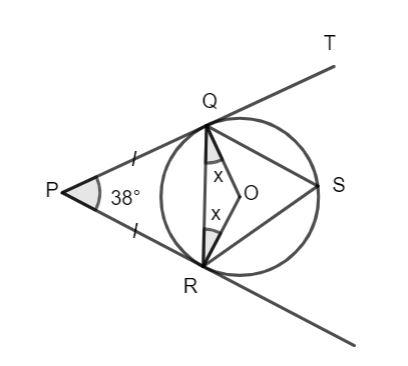
The tangent to the circle is the line that touches the circle only at one point.
The length of the tangents from the external point to the circle are equal.
Hence, the lengths of PQ and QR are equal to each other.
Hence, the triangle PQR is an isosceles triangle with side PQ equal to side PR, hence, the angle PQR and the angle PRQ are equal.
$$\mathrm{\angle }PQR=\mathrm{\angle }PRQ.........(1)$$
The value of angle QPR is given to be 38°.
The sum of angles of the triangle PQR is 180°. Then, we have:
$$\mathrm{\angle }PQR+\mathrm{\angle }PRQ+\mathrm{\angle }QPR={180}^{\circ }$$
$$\mathrm{\angle }PQR+\mathrm{\angle }PRQ+{38}^{\circ }={180}^{\circ }$$
Using equation (1), we have:
$$2\mathrm{\angle }PQR+{38}^{\circ }={180}^{\circ }$$
$$2\mathrm{\angle }PQR={180}^{\circ }-{38}^{\circ }$$
$$2\mathrm{\angle }PQR={142}^{\circ }$$
$$\mathrm{\angle }PQR={\displaystyle \frac{{142}^{\circ }}{2}}$$
$$\mathrm{\angle }PQR={71}^{\circ }...........(2)$$
From equation (1), we have:
$$\mathrm{\angle }PRQ={71}^{\circ }...........(3)$$
Let O be the center of the circle. The radius of the circle is always perpendicular to the tangent. Hence, OR is perpendicular to PR and OQ is perpendicular to PQ. Then, we have:
$$\mathrm{\angle }PRQ+\mathrm{\angle }ORQ={90}^{\circ }$$
Using equation (3), we have:
$${71}^{\circ }+\mathrm{\angle }ORQ={90}^{\circ }$$
$$\mathrm{\angle }ORQ={90}^{\circ }-{71}^{\circ }$$
$$\mathrm{\angle }ORQ={19}^{\circ }$$
$$\mathrm{\angle }OQR={19}^{\circ }$$
The value of angle QOR in triangle ORQ is given as follows:
$$\mathrm{\angle }QOR={180}^{\circ }-\mathrm{\angle }ORQ-\mathrm{\angle }OQR$$
$$\mathrm{\angle }QOR={180}^{\circ }-{19}^{\circ }-{19}^{\circ }$$
$$\mathrm{\angle }QOR={142}^{\circ }$$
The angle inscribed by a chord on the circle is half of the angle subtended at the center. Hence, the value of angle QSR is half of the angle QOR.
$$\mathrm{\angle }QSR={\displaystyle \frac{1}{2}}\mathrm{\angle }QOR$$
$$\mathrm{\angle }QSR={\displaystyle \frac{1}{2}}{.142}^{\circ }$$
$$\mathrm{\angle }QSR={71}^{\circ }..........(4)$$
It is given that angle PRS is equal to 111°.
Let's find angle SRQ.
$$\mathrm{\angle }PRQ+\mathrm{\angle }SRQ={111}^{\circ }$$
Using equation (3), we have:
$${71}^{\circ }+\mathrm{\angle }SRQ={111}^{\circ }$$
$$\mathrm{\angle }SRQ={111}^{\circ }-{71}^{\circ }$$
$$\mathrm{\angle }SRQ={40}^{\circ }............(5)$$
In triangle QRS, we have the sum of angles at 180°.
$$\mathrm{\angle }SRQ+\mathrm{\angle }RSQ+\mathrm{\angle }SQR={180}^{\circ }$$
Using equations (4) and (5), we have:
$${40}^{\circ }+{71}^{\circ }+\mathrm{\angle }SQR={180}^{\circ }$$
$${111}^{\circ }+\mathrm{\angle }SQR={180}^{\circ }$$
$$\mathrm{\angle }SQR={180}^{\circ }-{111}^{\circ }$$
$$\mathrm{\angle }SQR={69}^{\circ }...........(6)$$
PQT is a straight line, hence, the sum of the angles PQR, SQR, and TQS is 180°.
$$\mathrm{\angle }PQR+\mathrm{\angle }SQR+\mathrm{\angle }TQS={180}^{\circ }$$
From equations (2) and (6), we have:
$${71}^{\circ }+{69}^{\circ }+\mathrm{\angle }TQS={180}^{\circ }$$
$${140}^{\circ }+\mathrm{\angle }TQS={180}^{\circ }$$
$$\mathrm{\angle }TQS={180}^{\circ }-{140}^{\circ }$$
$$\mathrm{\angle }TQS={40}^{\circ }$$
Hence, the value of angle TQS is 40°.

Note: Note that, in the figure, the angle QRS looks like it is equal to RQS but it is not. You need to find them individually using the sum of angles of the triangles.