Question

PQRS shows walls of room each measuring \[8\,{\text{m}}\], such that wall PQ has a full length plane mirror. A camera is placed at M the midpoint of wall SR. In order to take clear image of point R, the camera should be placed at

A. \[4\,{\text{m}}\]
B. \[8\,{\text{m}}\]
C. \[16\,{\text{m}}\]
D. more than \[16\,{\text{m}}\]

Answer 1

Hint: Determine the path that the light from point R should travel to reach the camera at point M. The distance of this optical path is equal to the distance at which the camera should be placed. Using Pythagoras theorem, calculate the value of this distance of optical path of light from point R which gives the distance of the camera from point R.

Complete step by step answer:
We have given the length of each wall of the room is \[8\,{\text{m}}\].We have asked the distance at which the camera should be placed to take the clear image of the point R.We know that the clear image of any point can be obtained when the light from that object reaches the lens of the camera.In this case, the light from the point R (whose image is to be taken by the camera placed at point M) does not reach at the camera directly by travelling in the straight line.The light ray from point R need to reach the mirror on the wall PQ and then by reflection reach the camera M.

The distance of the optical path of the light rays from point R is as follows:

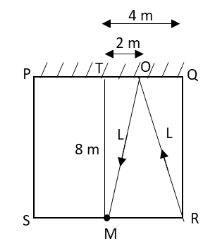
From the above diagram, we can see that the light from the point R has to travel a distance of \[2L\] which is the distance at which the camera should be placed.Let us first determine the value of \[L\].Apply Pythagoras theorem to the triangle MQT.
\[{L^2} = {\left( {8\,{\text{m}}} \right)^2} + {\left( {2\,{\text{m}}} \right)^2}\]
\[ \Rightarrow {L^2} = 64 + 4\]
\[ \Rightarrow {L^2} = 68\]
\[ \Rightarrow L = \sqrt {68} \]
\[ \Rightarrow L = 8.24\,{\text{m}}\]
Therefore, the distance at which the camera should be placed is
\[2L = 2\left( {8.24\,{\text{m}}} \right)\]
\[ \therefore 2L = 16.48\,{\text{m}}\]
Therefore, the cameral should be placed at more than \[16\,{\text{m}}\].

Hence, the correct option is D.

Note: The students should not forget to multiply the distance of the optical path of light from point R to the mirror by an integer 2 as the actual optical path is twice of this distance. If one forgets to multiply that distance by 2 then the final answer will be incorrect and at that distance the clear image of point R cannot be taken by the camera.