Question

PQRS is a square. Determine \[\angle SRP\].

Answer 1

Hint: Draw a rough diagram of a square named PQRS. Join diagonal PR and form two right-angle triangles PSR and PQR. Use S – S – S (side – side – side) congruency criteria to prove the two triangles congruent. Now, take the sum of \[\angle SRP\] and \[\angle QRP\] and equate it with \[{{90}^{\circ }}\] to find the value of \[\angle SRP\].

Complete step-by-step solution
Here, we have been provided with a square PQRS and we have to determine the measurement of \[\angle SRP\]. First, let us draw a rough diagram of a square.

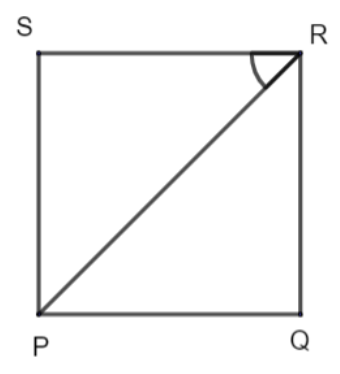
In the above figure, we have drawn a square PQRS with side PQ as the base. We have joined diagonal PR to form two right-angle triangles, namely PQR and PSR.
Now, in \[\Delta PQR\] and \[\Delta PSR\], we have,
PQ = PS - (sides of a square are equal)
QR = SR – (sides of a square are equal)
PR = PR - (common side)
So, we can say that \[\Delta PQR\] and \[\Delta PSR\] are congruent by S – S – S (side – side – side) congruency criteria. Therefore, we have,
\[\Rightarrow \angle SRP=\angle QRP\] - (1)
Now, we know that each angle of a square measure \[{{90}^{\circ }}\]. So, we have,
\[\Rightarrow \angle R={{90}^{\circ }}\]
Here, in the figure we can see that \[\angle R\] is made up of two angles namely \[\angle SRP\] and \[\angle QRP\]. Therefore, we get,
\[\Rightarrow \angle SRP+\angle QRP={{90}^{\circ }}\]
Using equation (1), we get,
\[\begin{align}
  & \Rightarrow \angle SRP+\angle QRP={{90}^{\circ }} \\
 & \Rightarrow 2\angle SRP={{90}^{\circ }} \\
 & \Rightarrow \angle SRP={{45}^{\circ }} \\
\end{align}\]
Hence, the measure of \[\angle SRP\] is \[{{45}^{\circ }}\].

Note: One may note that here in the above solution we have used S – S – S congruency criteria to prove the two triangles congruent. You may use R – H – S (Right – Hypotenuse – Side) congruency criteria also for the same result. The above result must be remembered as a property of a square that ‘diagonals of a square bisect the opposite angles.’ In many places, we need to use this property directly. Note that while solving the question you must draw the diagram otherwise you will get confused.