Question

PQRS is a rhombus with \[\angle PQR = 58^\circ \]. Determine \[\angle PRS \].

Answer 1

Hint: The quadrilateral having all sides of equal length is called rhombus. The adjacent sides of a rhombus are supplementary. The diagonal of a rhombus is angular bisector.

Complete step-by-step answer:
Consider a rhombus \[PQRS\] inside of a circle as shown below.

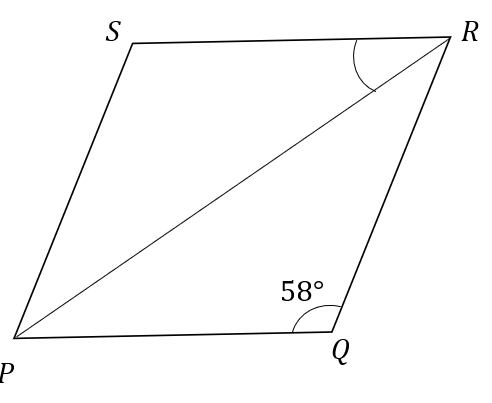
Since, the adjacent sides of a rhombus are supplementary, it can be written as follows:

\[
  \angle QRS + \angle PQR = 180^\circ \\
  \angle QRS = 180^\circ - \angle PQR \\
  \angle QRS = 180^\circ - 58^\circ \\
  \angle QRS = 122^\circ \\
\]

Since, the diagonal of a rhombus is angular bisector, so the \[\angle PRS \] is half of the\[\angle QRS\].
\[
  \angle PRS = \dfrac{{\angle QRS}}{2} \\
  \angle PRS = \dfrac{{122^\circ }}{2} \\
  \angle PRS = 61^\circ \\
\]
Thus, the value of the \[\angle PRS \] is \[61^\circ \].

Note: The adjacent sides of a rhombus are supplementary and the diagonal of a rhombus is angular bisector. These two properties should be known to students to solve this problem.