Question

PQRS is a rectangle. If $PQ+QR=7$ and $PR+QS=10$ , find the area of the rectangle PQRS.

Answer 1

Hint: First we will write down the definition and properties of a rectangle. We will find the length of a diagonal PR first as the two diagonals bisect each other. Then we will take the given rectangle and take one triangle that is PQR. Then we will apply the Pythagoras theorem to find the length and the breadth of the rectangle and finally apply the formula $\left( \text{length}\times \text{breadth} \right)$to find the area of the rectangle.

Complete step by step answer:
First of all, let’s understand what a rectangle is. So, a rectangle is a two-dimensional figure, which has four sides (Quadrilateral) and four vertices. All the interior angles of the rectangle are equal which measure ${{90}^{\circ }}$ . The opposite sides of a rectangle are equal and are parallel.
Now, let’s look at some of the properties of a rectangle:
A. The area of a rectangle is defined by the product of the length and breadth that means the product of adjacent sides. Therefore, Area of a rectangle $=\left( \text{length}\times \text{breadth} \right)$ square units,
B. The perimeter of a rectangle is the sum of all four sides. Since opposite sides are equal in a rectangle, therefore: The perimeter of a rectangle $=2\left( \text{length}+\text{breadth} \right)$ units.
C. The diagonals of a rectangle are of equal length and bisect each other.

Now, let’s take the information given in the question, we are given that PQRS is a rectangle , which will look like the following figure:
 

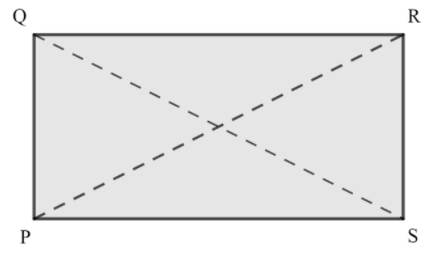
Now, it is given that $PQ+QR=7$ and $PR+QS=10$. Here, as we can see that PQ and QR are the breadth and length of the rectangle and PR, QS are the diagonals of the rectangle.
Now, according to the properties of a rectangle we know that the diagonals of a rectangle are of equal length, therefore: $PR=QS$ . Now, we will put this value in the equation given in the question that is: $PR+QS=10$ , therefore we will get: $\Rightarrow PR+PR=10\Rightarrow 2PR=10\Rightarrow PR=\dfrac{10}{2}\Rightarrow PR=5\text{ }.......\left( 1 \right)$
Now, let’s take the triangle PQR , we know that interior angles of a rectangle are ${{90}^{\circ }}$ , therefore PQR is a right angled triangle which is right angled at Q.
Now, we are given that $PQ+QR=7$ which gives us: $PQ=7-QR\text{ }.......\left( 2 \right)$ ,
Now we will apply the Pythagoras theorem in triangle PQR. We know that according to the Pythagoras theorem: ${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Perpendicular \right)}^{2}}$
Now, in PQR, we have PQ as our base , QR as perpendicular and PR as the hypotenuse, therefore: $P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}$ , now we will put the values of PR and PQ from equation 1 and 2 respectively:
Therefore: ${{\left( 5 \right)}^{2}}={{\left( 7-QR \right)}^{2}}+Q{{R}^{2}}$
We will now apply the identity \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\] on the RHS, then we will get: $\begin{align}
  & \Rightarrow {{\left( 5 \right)}^{2}}=\left( {{7}^{2}}+Q{{R}^{2}}-14QR \right)+Q{{R}^{2}} \\
 & \Rightarrow 25=49+Q{{R}^{2}}-14QR+Q{{R}^{2}} \\
 & \Rightarrow 0=49+2Q{{R}^{2}}-14QR-25 \\
 & \Rightarrow 2Q{{R}^{2}}-14QR+24=0 \\
\end{align}$
Now, we will take 2 common from the equation and then we will get:
$\begin{align}
  & \Rightarrow 2\left( Q{{R}^{2}}-7QR+12 \right)=0 \\
 & \Rightarrow Q{{R}^{2}}-7QR+12=0 \\
\end{align}$
Now, we will split the middle term to solve the given quadratic equation:
$\begin{align}
  & \Rightarrow Q{{R}^{2}}-7QR+12=0 \\
 & \Rightarrow Q{{R}^{2}}-4QR-3QR+12=0 \\
 & \Rightarrow QR\left( QR-4 \right)-3\left( QR-4 \right)=0 \\
 & \Rightarrow \left( QR-4 \right)\left( QR-3 \right)=0 \\
\end{align}$
Therefore the length of QR is either 4 or 3 . Now, if QR is 4 then from equation 2 we know that $PQ=7-4=3$ .
Now, let’s take the first case where the length of the rectangle that is QR is 4 and the breadth that is PQ is 3, now we know that the area of the rectangle $=\left( \text{length}\times \text{breadth} \right)$ square units,
Therefore, the area of PQRS $=\left( 4\times 3 \right)=12$ square units.
Now, in the second case when the length of the rectangle that is QR is 3 and the breadth that is PQ from equation 2: $PQ=7-3=4$
Therefore, the area of PQRS $=\left( 3\times 4 \right)=12$ square units.

Hence, the answer of the question is 12 square units.

Note: As we saw we got the quadratic equation in QR, always consider all the cases. Students might get confused between the area and the perimeter; remember that an area is the space enclosed by the shape whereas the perimeter is the boundary of the shape.