Question

PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm, then find QN if PS = 8 cm.

  

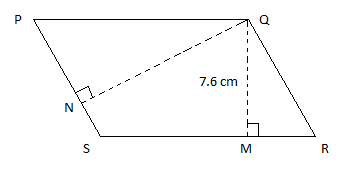
Answer 1

Hint: Remember that a parallelogram has two adjacent sides which may be of unequal lengths. The area of the parallelogram can be calculated by using any on these adjacent sides and its corresponding height.
The values of area obtained in both the cases must be the same (because it is the same parallelogram). Using this fact, form an equation and solve.

Complete step-by-step answer:
Let's say that the length of QN is x cm.

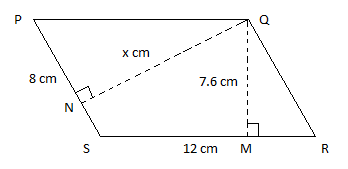
We know that the area of a parallelogram is equal to b × h, where b (base) is the length of one of the equal pair of opposite sides and h is the height between them.
Therefore, considering the area of PQRS, once with the base SR and once with the base PS, we get:
Area = SR × QM = PS × QN
Using the given values, we have:
⇒ 12 × 7.6 = 8 × QN
⇒ QN = $\dfrac{12\times 7.6}{8}$ = 3 × 3.8 = 11.4
Therefore, the length of QN is 11.4 cm.
Note: Area is measured by counting the number of squares of a unit length present in a shape. There are a × a unit squares inside a square of side a units.
Area of a parallelogram is the same as the area of a rectangle with base b units and height h units, that is b × h square units.
It is possible to draw a parallelogram around a triangle such that one of the sides of the triangle acts as its diagonal. Since the diagonal divides a parallelogram into two identical triangles, the area of a triangle is equal to $\dfrac{1}{2}$ × b × h, half of the area of the parallelogram which has a same base and the same corresponding height.