Question

PQRS is a parallelogram bisectors of \[\angle P\] and \[\angle Q\] meet at O. What is the measure of \[\angle POQ\].

Answer 1

Hint:
Here, we will first form the equation between the angles which are bisected. Then we will find the value of the sum of the two angles of the triangle PQO. We will then subtract that sum from \[180^\circ \] to get the value of \[\angle POQ\].

Complete step by step solution:
It is given that bisectors of \[\angle P\] and \[\angle Q\] meet at O. Therefore we will draw the diagram of the parallelogram with the given conditions.

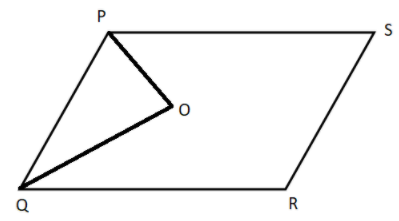
Now we will form the relation between the bisected angles. Therefore, we get
\[\angle SPO = \angle OPQ\] and \[\angle RQO = \angle OQP\]…………………\[\left( 1 \right)\]
We know that the property of the parallelogram that the sum of the two adjacent angles of the parallelogram is equal to \[180^\circ \]. Therefore, we get
\[ \Rightarrow \angle P + \angle Q = 180^\circ \]…………………\[\left( 2 \right)\]
We know that \[\angle P = \angle SPO + \angle OPQ\] and \[\angle Q = \angle RQO + \angle OQP\]. Therefore, we get
\[ \Rightarrow \left( {\angle SPO + \angle OPQ} \right) + \left( {\angle RQO + \angle OQP} \right) = 180^\circ \]
Now substituting the equation \[\left( 1 \right)\] in the equation \[\left( 2 \right)\], we will find the value of the sum of the angles \[\angle OPQ\] and \[\angle OQP\]. Therefore, we get
\[ \Rightarrow \left( {\angle OPQ + \angle OPQ} \right) + \left( {\angle OQP + \angle OQP} \right) = 180^\circ \]
Adding the terms, we get
\[ \Rightarrow \left( {2\angle OPQ} \right) + \left( {2\angle OQP} \right) = 180^\circ \]
Simplifying the above equation, we get
\[ \Rightarrow 2\left( {\angle OPQ + \angle OQP} \right) = 180^\circ \]
\[ \Rightarrow \angle OPQ + \angle OQP = \dfrac{{180^\circ }}{2} = 90^\circ \]…………………\[\left( 3 \right)\]
We know that in the triangle \[PQO\], the sum of all the angles is equal to \[180^\circ \]. Therefore, we get
\[ \Rightarrow \angle POQ + \angle OPQ + \angle OQP = 180^\circ \]
Now by using the equation \[\left( 3 \right)\] in the above equation, we get
\[ \Rightarrow \angle POQ + 90^\circ = 180^\circ \]
\[ \Rightarrow \angle POQ = 180^\circ - 90^\circ = 90^\circ \]

Hence the measure of \[\angle POQ\] is \[90^\circ \].

Note:
Geometry is the branch of mathematics that deals with points, lines and shapes. In geometry, bisection is the division of something into two equal parts. Bisection is generally done with a line which is called a bisector. There are two main types of bisectors i.e. line segment bisector and angle bisector.
A line segment bisector is a line or line segment that divides the line into two equal parts or which passes through the midpoint of the line segment.
Angle bisector is the line or line segment that divides an angle into two equal parts. An angle has only one bisector. Also there are two types of angle bisectors i.e. interior and exterior angle bisector.