Question

PQRS is a parallelogram and M, N are the midpoints of PQ and RS respectively. Which of the following is not true.

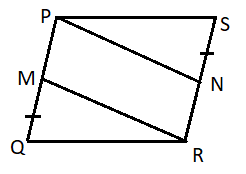
$\left( a \right)$ RM trisects QS
$\left( b \right)$ PN trisects QS
$\left( c \right)\Delta PSN \sim \Delta QMR$
$\left( d \right)$ MS is not parallel to QN

Answer 1

Hint: In this particular question use the concept that in a parallelogram opposite sides are parallel to each other and are of equal length, so if two lines are parallel to each other and are of equal length so they make a parallelogram, so use these concepts to reach the solution of the question.

Complete step by step solution:
Given data:
PQRS is a parallelogram as shown in the question figure.
It is also given that M and N are the midpoints of PQ and RS.
Now as we all know that in a parallelogram opposite sides are parallel to each other and are of equal length.
Therefore, in the given parallelogram PQRS, PQ||RS and PS||QR.
Now it is given that M and N are the midpoints of line PQ and RS as shown in the figure.
Therefore, PM = MQ
And SN = RN
As PQ = SR
Therefore, MQ = SN................... (1)
As PQ||RS,
So MQ||SN................. (2)

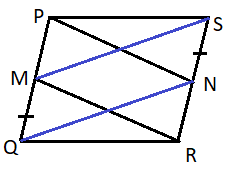
Now join M and S, and Q and N as shown in the above figure.
So according to the condition of parallelogram and from the equation (1) and (2) quadrilateral MSNQ as shown in the figure is also a parallelogram.
So sides MS and QN are parallel to each other.
So this is the required answer.
Hence option (D) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall all the conditions of the parallelogram which is stated above, so by using these properties first prove that MQ and SN are of equal length and parallel to each other as above, so MSNQ form a parallelogram so that MS and QN are parallel to each other.