Question

PQRS and ABRS are parallelogram and X is any point on the side BR. Show that
I.$ar\,\left( PQRS \right)=ar\,\left( ABRS \right)$
II.$ar\,\left( AXS \right)=\dfrac{1}{2}ar\,\left( PQRS \right)$

Answer 1

Hint: A parallelogram is a four sided rectilinear figure with opposite sides parallel. It's a simple quadrilateral with two pairs of parallel sides. The opposite facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure.

Complete step-by-step answer:

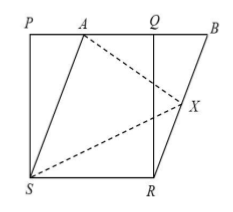
 PQRS and ABRS are parallelogram
$ar\,\left( PQRS \right)=ar\,\left( ABRS \right)$
Now,
Since PQRS is a parallelogram,
Therefore, the opposite side of the parallelogram are parallel.
Thus,
$PQ\parallel RS$
And ABRS is also a parallelogram,
So,
$AB\parallel RS$ (Opposite side of a parallelogram are parallel)
Now,
Since $PQ\parallel RS$ and $AB\parallel RS$
We can say that $PB\parallel RS$
Now, we know that
PQRS and ABRS are two parallelograms with same base RS
And between the same parallel PB and RS
Thus, we can say that
$ar\,\left( PQRS \right)=ar\,\left( ABRS \right)$
Since,
Parallelograms with the same base and between the same parallels are equal in area.

$ar\,\left( AXS \right)=\dfrac{1}{2}ar\,\left( PQRS \right)$
Since, ABRS is a parallelogram
$AS\parallel BR$ (Opposite side of parallelogram are parallel)
Now, we know,
$\Delta $AXS and parallelogram ABRS lie on the same base AS and between the same parallel lines AS and BR,
$\therefore $$ar\,\left( AXS \right)=\dfrac{1}{2}ar\,\left( ABRS \right)$
(Area of triangle is half of parallelogram if they have the same base and between same parallels)
We have above that
$ar\,\left( PQRS \right)=ar\,\left( ABRS \right)$
$ar\,\left( AXS \right)=\dfrac{1}{2}ar\,\left( PQRS \right)$
Hence proved

Note: In this type of questions students often forget to draw the diagram but remember the drawing diagram is as important as solving. The diagram gives you the rough idea of how to proceed and what you have to proceed with.