Question

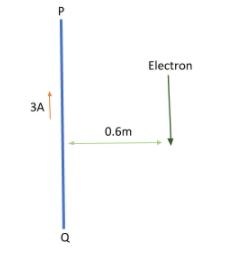
PQ is a long straight conductor carrying a current of 3A as shown in the figure. An electron moves with a velocity of $2 \times 10^7 ms^{-1}$ parallel to it. Find the force acting on the electron.

Answer 1

Hint: Remember that a current carrying conductor produces a magnetic field. And this magnetic field is responsible for the magnetic force experienced by the moving electron. Use Fleming’s right hand rule to verify that the velocity and the magnetic field vectors are perpendicular to each other.

Formula used:
$\vec{F} = q\;(\vec{v} \times \vec{B})$ : magnetic force exerted by a current carrying conductor
Magnetic flux or field strength $B = \dfrac{\mu_{0} \times I}{2 \pi d}$ where $\mu_{0}$ is the magnetic permeability of vacuum, I is the current flowing through the conductor, d is the distance between the conductor and the electron.
$\mu_{0} = 4 \pi \times 10^{-7} T\;m\;A^{-1}$

Complete step-by-step answer:
Let us begin deconstructing our question.
We have a current carrying conductor through which a current of 3A is passing. Now, we know that a current carrying conductor produces a magnetic field around it. If you hold up your thumb along the direction of the current and close your fist, all the other fingers point to the direction of the magnetic field around it.
We are asked to find the force exerted by the magnetic field that is acting on the electron, which can be quantified as:
$\vec{F} = q\;(\vec{v} \times \vec{B}) = q\;v\;B\;sin \theta$ where $\theta$ is the angle between the velocity and the field strength vector. Here, from Fleming’s right hand rule, we get that $\theta = 90^{\circ}$.
The magnetic field is given by the formula:
$B = \dfrac{\mu_{0} \times I}{2 \pi d}$
$\Rightarrow B = \dfrac {4 \pi \times 10^{-7} \times 3}{2 \times \pi \times 0.6} = 10 \times 10^{-7}\; T = 10^{-6}\; T$
Therefore,
$\vec{F} = q\;v\;B\;sin \theta = 1.6 \times 10^{-19} \times 2 \times 10^7 \times 10^{-6} \times sin (90^{\circ}) = 3.2 \times 10^{-18}\;N$
Thus the electron experiences a force of $3.2 \times 10^{-18}\;N$

Note: It is important that the sine of the angle between the velocity and magnetic field vectors is a finite value, following which you may not get the required result of an existing directional field. If the angle between them is zero, it means that there is no magnetic force exerted in that direction.
Also note that the right hand thumb rule is used to determine the direction of the magnetic field produced by a current carrying conductor whereas Fleming’s right hand rule is used to determine the direction of the velocity and magnetic field vectors and the corresponding force produced by them