Question

PQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If $PQ=16$ cm and $RS=12$ cm. Then find the distance between PQ and RS, if they lie.
(i) on the same side of the centre O. (ii) on the opposite of the centre O.

A. 8 cm and 14 cm
B. 4 cm and 14 cm.
C. 2 cm and 14 cm
D. 2 cm and 28 cm.

Answer 1

Hint: We use the image to find out the relation between the two parts. We also use the theorem of chord bisection of a circle. Using Pythagoras’ theorem, we find out the values of the distance between PQ and RS.

Complete step-by-step answer:
We first place the given details of $PQ=16$ cm and $RS=12$ cm, O is the centre of the circle in an image of a circle. The radius of the circle is 10 cm. We draw a perpendicular line from the centre O on both PQ and RS. They cut the chords at points M and N respectively. So, $\angle ONS=\angle OMQ={{90}^{\circ }}$ as $OM\bot PQ,ON\bot RS$.
We know that the perpendicular line from the centre of a circle on a chord of the circle bisects the chord.
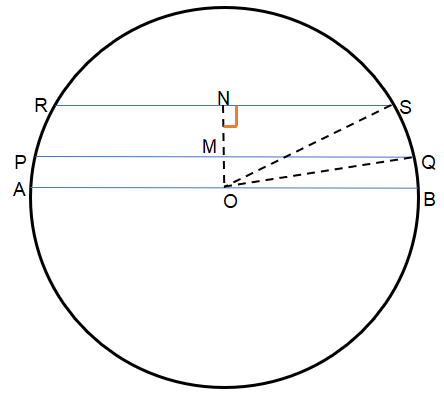
In the first image the chords PQ and RS are on the same side of the centre.
 

In the second image the chords PQ and RS are on the opposite sides of the centre.

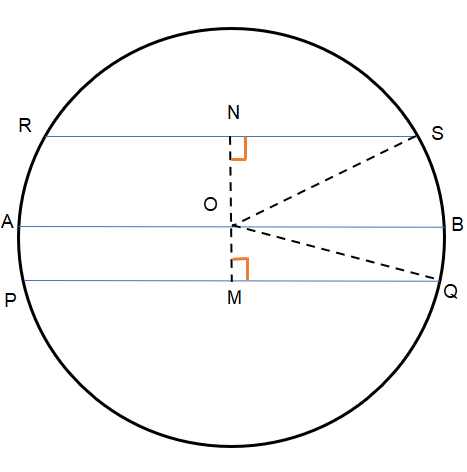
Now OS and OQ are the radius. So, $OS=OQ=10$. OM and ON bisects the chords PQ and RS. So, $PM=MQ=\dfrac{1}{2}PQ=\dfrac{16}{2}=8$ and $RN=NS=\dfrac{1}{2}RS=\dfrac{12}{2}=6$.
So, we got two right-angle triangles in the form of $\Delta ONS,\Delta OMQ$.
Using Pythagoras’ theorem, we get ${{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}={{\left( hypotenuse \right)}^{2}}$.
So, for those two triangles $\Delta ONS$ and $\Delta OMQ$ we got ${{\left( ON \right)}^{2}}+{{\left( NS \right)}^{2}}={{\left( OS \right)}^{2}}$ and ${{\left( OM \right)}^{2}}+{{\left( MQ \right)}^{2}}={{\left( OQ \right)}^{2}}$ respectively.
We put the values to get
$\begin{align}
  & {{\left( ON \right)}^{2}}+{{\left( NS \right)}^{2}}={{\left( OS \right)}^{2}} \\
 & \Rightarrow {{\left( ON \right)}^{2}}+{{\left( 6 \right)}^{2}}={{\left( 10 \right)}^{2}} \\
 & \Rightarrow {{\left( ON \right)}^{2}}=100-36=64={{8}^{2}} \\
 & \Rightarrow ON=8 \\
\end{align}$
and
 $\begin{align}
  & {{\left( OM \right)}^{2}}+{{\left( MQ \right)}^{2}}={{\left( OQ \right)}^{2}} \\
 & \Rightarrow {{\left( OM \right)}^{2}}+{{\left( 8 \right)}^{2}}={{\left( 10 \right)}^{2}} \\
 & \Rightarrow {{\left( OM \right)}^{2}}=100-64=36={{6}^{2}} \\
 & \Rightarrow OM=6 \\
\end{align}$
Now we will have two answers for two different images.
The distance between PQ and RS is MN which is equal to $MN=ON\pm OM$.
Putting values, we get $MN=ON\pm OM=8\pm 6=14,2$
The value of 14 is for the first image where PQ and RS are on the same side of the centre and the value of 2 is for the second image where PQ and RS are on the opposite sides of the centre.
The correct option is C.

So, the correct answer is “Option C”.

Note: The only change in the two parts is that when we are trying to find the distance. In one case we are adding the distance and subtracting in the other one. The theorem is also applicable for chords which are oblique in nature. It works because of the chords being parallel to each other.