Question

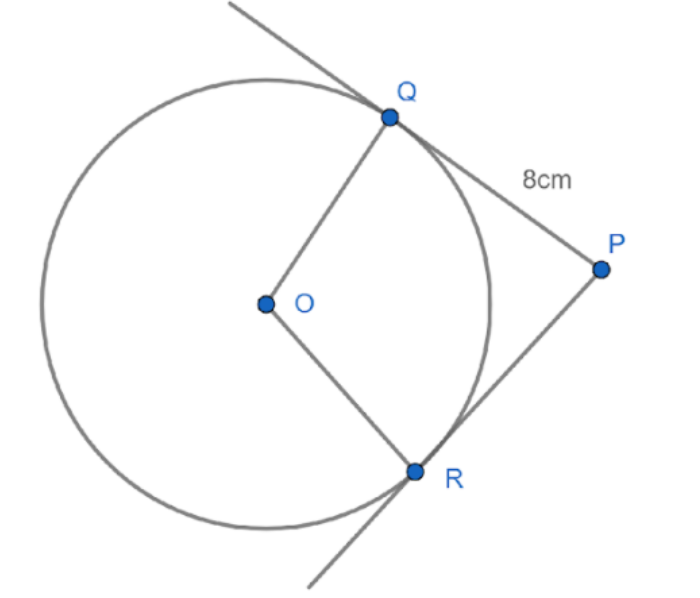
PQ and PR are the tangents to a given circle as shown in the figure. If $ \angle RPQ = {90^ \circ } $ and $ PQ = 8cm $ , find the radius of the circle (in cm)

Answer 1

Hint: The given question asks us to find the radius of the given circle in cm. We are given the angles $ \angle RPQ = {90^ \circ } $ as well as the length of one tangent, the first important theorem to remember to solve this question is to know that the two tangents of a circle to the same points are equal in size so the side PR would also be the same as the size of the side PQ given as $ PQ = 8cm $ . The next important thing to note is that the angle the tangent makes with the normal (the segment from the tangent to the centre of the circle) is a right angle.

Complete step-by-step answer:
The angle RPQ is given as,
 $ \angle RPQ = {90^ \circ } $
The one tangent is given as,
 $ PQ = 8cm $
The other tangent will also be equal, and its values will
 $ RP = 8cm $
The angles $ \angle PQO $ and $ \angle PRO $ are also right angles because the angle the normal makes with the tangent is a right angle and the $ QO $ and $ RO $ are normal to the tangents at $ R $ and $ Q $
The quadrilateral $ PQOR $ has three right angles; the fourth angle will also be a right angle so as to make the sum the total of $ {360^ \circ } $ . Hence this is a square whose side is $ 8cm $ , which means the radius of the circle will also be $ 8cm $ .
So, the correct answer is “8 cm”.

Note: There is a very important conclusion which could have helped us to solve this question easily which is that the centre of the circle along with two points from which the circle is drawn and the intersection of the circles form a cyclic quadrilateral, which means sum of the opposite angles is $ {180^ \circ } $ . This phenomenon can be easily seen in the question above and would have cut our solution by half.