Question

Potential difference between A & B in the given branch of a circuit is

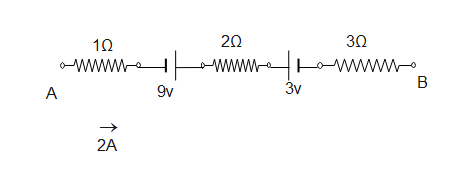
A) 6V
B) 12V
C) 9V
D) 0V

Answer 1

Hint: We have to observe given diagram there is shown a 2A current is flowing through In the direction A to B. here we have to find the potential difference between A & B, we denoted as ${V_{AB}}$ . we know that the voltage will drop due to resistor we can clearly understand by the ohm's law.

Complete step by step solution:
A 2A current is flowing through In the direction A to B as shown in the circuit. We know that ohm's law, which states that the strength of a direct current is directly proportional to the potential difference and inversely proportional to the resistance of the circuit or we can write $V = IR$. In the circuit there is mentioned a current and resistance so we can write accordingly. For the first resistor there is 1 $\Omega $ and 2A current is flowing so we can write $2 \times 1$. Next there is a negative terminal of the battery its 9 volt so we consider –9v. Similarly there is 2 $\Omega $ resistor and 2A current hence we can write $2 \times 2$. Finally this current flows into the positive terminal of the battery its 3 volt and with the consideration of current and resistor we write $2 \times 3$ like this way we completed the loop.
Now, in mathematical form.
$\eqalign{
  & {V_{AB}} = 2 \times 1 - 9 + 2 \times 2 + 3 + 3 \times 2 \cr
  & \Rightarrow {V_{AB}} = 2 - 9 + 4 + 3 + 6 \cr
  & \Rightarrow {V_{AB}} = 2 + 4 \cr
  & \therefore {V_{AB}} = 6V \cr} $

Hence, the correct option is A.

Note:
Sometimes circuits have branches, in these cases we have to follow the same procedure to find potential difference by applying ohm's law, for this we have to observe the given circuit clearly. We know that Ohm's law states that the voltage or potential difference between two points is directly proportional to the current directly proportional to the resistance of the circuit.