Question

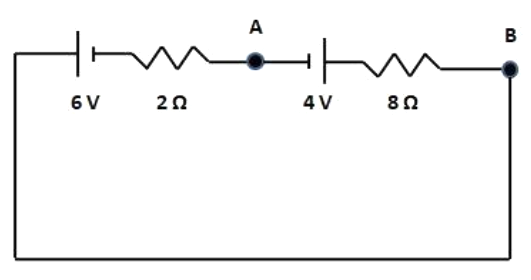
Potential difference between \[A\] and \[B\] in the following circuit is:

a. \[2.8V\]
b. \[4V\]
c. \[6V\]
d. \[5.6V\]

Answer 1

Hint: We will calculate the current through the circuit and then will try to find the resultant potential difference between these two points.

Formula Used:
Kirchhoff’s loop rule states that the sum of all the electric potential differences between the points in a loop is always zero.
\[\sum {{V_A}} = \sum {{V_B}} \].
According to the Ohm’s law,
Potential difference in a loop is equal to the production of current flows in the circuit and the resistance of the loop.
So, \[V = I.R\], where \[V\] is a potential difference, \[I\] is current flows, \[R\] is resistance.

Complete step by step answer:
First of all we will calculate the current flows in the circuit.
So, current flow in the circuit is the ratio of net volt and the ratio of the net resistance in the circuit.
Two terminals of the battery of \[6V\] and \[4V\] are connected.
So, the net potential differences between these two terminals is \[ = (6 - 4)V = 2V\] .
Now, the net resistance in the circuit is \[ = (8 + 2)\Omega = 10\Omega \] .
So, applied current flow \[(I)\]\[ = \dfrac{{2V}}{{10\Omega }} = 0.2A\]
Now, according to Kirchhoff’s loop rule, net potentiality in point \[A\]and \[B\] must be equal to zero.
So, Current flow through the\[8\Omega \] resistor is \[0.2A\] but the potentiality on that resistor will be\[ = (0.2 \times 8) = 1.6\].
But the terminal at point \[A\]has a potentiality of \[4V\].
So, the resultant potential difference from point \[A\]to point \[B\] would be equal.
So, moving from point \[A\] to point \[B\], the following equation must be stated:
\[{V_A} + 4 + 1.6 = {V_B}\]
Add the values in L.H.S, we get:
\[{V_A} + 5.6 = {V_B}\]
Now, taking the variable \[{V_A}\]to the R.H.S, we get:
\[{V_B} - {V_A} = 5.6\]
So, the potential difference between \[A\] and \[B\] is\[5.6\Omega \]

Hence, the correct answer is option (D).

Note: Potential difference (voltage) between two points is the net difference of electrical potential between these two points. Kirchhoff’s loop law directed that the sum of the potential differences (voltage) around any closed circuit is always zero.