Question

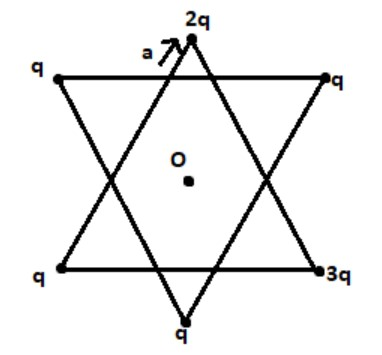
Positive point charges are placed at the vertices of a star shape as shown in the figure. Direction of the electrostatic force on a negative point charge at the centre O of the star is:

A. Neither along horizontal or vertical direction
B. Vertically up
C. Towards left
D. Vertically down

Answer 1

Hint: We have to use the superposition principle to find the net electrostatic force on the charge kept at the center of the star structure.

Complete step by step solution:
Electrostatic force between two charges $q\text{ and }2q$ is the resultant of the force between the system of two combination of charge $\left( q,q \right)\text{ and }\left( q,q \right)$
Using symmetry of the structure,
If all the vertices have the same charge $q$ then the net force on the charge kept at the center is zero.
The remaining charge $\left( 2q-q=q \right)$on the top will apply force in vertically upward direction and the remaining charge $\left( 3q-q=2q \right)$will apply force along the vertices having charge $2q$.
As we know that the magnitude of force is given as $F=\dfrac{K{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}$
Angle between force towards vertically up and the force towards $3q$vertex is $120{}^\circ $
Therefore, the resultant force will be in between the top and $3q$ vertex.

Hence, the direction of net force is neither horizontal nor the vertical.

Note: The principle of superposition states that every charge in space creates an electric field at point independent of the presence of other charges in that medium. The resultant electric field is a vector sum of the electric field due to individual charges.