Question

What is the positive and negative angle that is co – terminal with $-{{150}^{\circ }}$?

Answer 1

Hint: First we will understand the meaning of the term co – terminal angle with the help of a diagram. We will assume the given angle as $\theta $. Now, to find the positive co – terminal angle will add the angle ${{360}^{\circ }}$ in $\theta $ while to find the negative co – terminal angle we will subtract the angle ${{360}^{\circ }}$ from $\theta $. The two angles obtained will be our answer.

Complete step by step answer:
Here we have been given an angle of measurement $-{{150}^{\circ }}$ and we are asked to find its positive and negative co – terminal angle. First we need to understand the meaning of the term co – terminal angle.
Now, in mathematics two angles are said to be co – terminal angles when they have their initial side and the terminal side in the same position and direction.

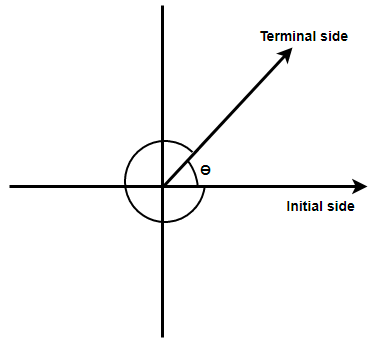
For an angle $\theta $ we have a negative co – terminal angle and a positive co – terminal angle. If we will consider the angle $\left( \theta -{{360}^{\circ }} \right)$ then we will see that its initial and the terminal side overlaps with those of the angle $\theta $. Similarly, when we will consider the angle $\left( \theta +{{360}^{\circ }} \right)$ its initial and terminal side will again overlap with those of the angle $\theta $. Here, $\left( \theta -{{360}^{\circ }} \right)$ is the negative co – terminal angle and $\left( \theta +{{360}^{\circ }} \right)$ is the positive co – terminal angle.
Now, let us come to the question. Assuming the angle $-{{150}^{\circ }}$ as $\theta $ we have,
$\Rightarrow $ Negative co – terminal angle = $\left( -{{150}^{\circ }}-{{360}^{\circ }} \right)=\left( -{{510}^{\circ }} \right)$
$\Rightarrow $ Positive co – terminal angle = $\left( -{{150}^{\circ }}+{{360}^{\circ }} \right)=\left( {{210}^{\circ }} \right)$
Hence, the above two values obtained are our answer.

Note: Note that you can also find the measure of the required angles in the unit radian. What you have to do is multiply the given angle $\theta $ with $\dfrac{\pi }{{{180}^{\circ }}}$ to cancel the unit degree and convert it into radian. Now, add the angle $2\pi $ in it to get the positive co – terminal angle and subtract the angle $2\pi $ from $\theta $ to get the negative co – terminal angle.