Question

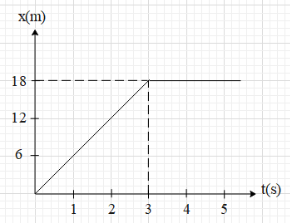
Position-time graph of a body of mass 5 kg is given in the diagram. The impulse on body at $t=3s$ is

A. $30\widehat{i}kgm{{s}^{-1}}$
B. $-30\widehat{i}kgm{{s}^{-1}}$
C. $6\widehat{i}kgm{{s}^{-1}}$
D. $-6\widehat{i}kgm{{s}^{-1}}$

Answer 1

Hint: Analyse the given graph. Check what is happening to the motion of the body before time $t=3s$ and after time $t=3s$ and calculate the velocities before and after $t=3s$. Then use the formula for impulse and calculate the impulse on the body at $t=3s$.

Formula used:
$v=\dfrac{\Delta x}{\Delta t}$
where v is the constant velocity of a body with change in position of $\Delta x$ in a time interval of $\Delta t$.
$\Delta P=m\left( {{v}_{2}}-{{v}_{1}} \right)$
where $\Delta P$ is the impulse on a body of mass m when its velocity change from ${{v}_{2}}$ to ${{v}_{1}}$.

Complete step by step answer:
For the given figure, we can see that the graph of position – time graph of the body shows a straight line before time $t=3s$. This means that the position of the body is changing uniformly with respect to time. Therefore, the body is travelling with constant velocity before time $t=3s$.With this, the speed of the body before $t=3s$ is ${{v}_{1}}=\dfrac{\Delta x}{\Delta t}$ … (i)
From the graph, we get that $\Delta x=18m$ and $\Delta t=3s$.
Substitute these values in equation (i).
$\Rightarrow {{v}_{1}}=\dfrac{18}{3}=6m{{s}^{-1}}$
Now, in the graph we can see that just after time $t=3s$ the position of the body remains constant with respect to time. This means that the body comes to rest at time $t=3s$, and remains at rest. Since the body is at rest, its velocity is zero i.e. ${{v}_{2}}=0$.

This means that at time $t=3s$, the velocity of the body change from ${{v}_{1}}=6m{{s}^{-1}}$ to ${{v}_{2}}=0$.
Therefore, the impulse on the body at $t=3s$ is $\Delta P=m\left( {{v}_{2}}-{{v}_{1}} \right)=5\left( 0-6 \right)=-30kgm{{s}^{-1}}$.
Now, since the body’s position is increasing along the x-axis, we can write the impulse in vector form as $-30\widehat{i}kgm{{s}^{-1}}$.

Hence, the correct option is B.

Note: Some of the students may not know what is meant by impulse created on a body Impulse on a body is the change in momentum created in a body.Note that it is final momentum minus initial momentum. Some students may make a mistake by subtracting the initial momentum from the final momentum.