Question

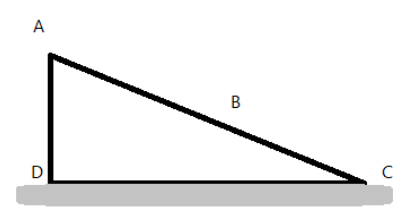
Portion AB of the wedge shown in the figure is rough and BC is smooth. A solid cylinder rolls without slipping from A to B. If $AB=BC$, then ratio of translational kinetic energy to rotational kinetic energy, when the cylinder reaches point C is then,

\[\begin{align}
  & A.\dfrac{3}{5} \\
 & B.5 \\
 & C.\dfrac{7}{5} \\
 & D.\dfrac{8}{3} \\
\end{align}\]

Answer 1

Hint: We know that rolling involves both rotation along the axis and translation in one direction of the object. When the surface is smooth or ideal the body does not slide along the surface. Also during rotational motion, the body undergoes linear and rotational acceleration.
Formula: $K_{T}=\dfrac{1}{2}mv_{f}$ and $K_{R}=\dfrac{I\omega^{2}}{2}$

Complete answer:
Given that the AB is rough, then we can say that the object will experience friction, when passing through this region, similarly, BC is smooth, then the body will not experience any friction, when rolling through this surface.
Let the height from A to B be $h$, since the rolling body is a solid cylinder of mass $m$ with angular velocity $\omega=\dfrac{v}{R}$, where $v$ is the translational velocity, and $R$ is the radius of the solid cylinder, we can say that the body also experiences moment of inertia. From the law of conservation of energy we can say that, the potential energy due to height $h$ is transferred into the kinetic energy and the rotational energy, this can be written as
$mgh=\dfrac{mv^{2}}{2}+\dfrac{mR^{2}}{2}\dfrac{v^{2}}{R^{2}}$
$\implies gh=\dfrac{v^{2}}{2}+\dfrac{v^{2}}{4}$
$\implies gh=\dfrac{3v^{2}}{4}$
$\implies v=\sqrt{\dfrac{4gh}{3}}$
Where $v$ is the velocity at B.
Then, $\omega=\dfrac{1}{R}\sqrt{\dfrac{4gh}{3}}$
In the region BC, only translational energy there, then we get,
$mgh=\dfrac{1}{2}m\Delta v^{2}$
$\implies gh=\dfrac{v_{f}^{2}-\left(\sqrt{\dfrac{4gh}{3}}\right)^{2}}{2}$
$\implies 2gh=v_{f}^{2}-{\dfrac{4gh}{3}}$
$\implies v_{f}^{2}=2gh+\dfrac{4gh}{3}$
$\implies v_{f}^{2}=\dfrac{10gh}{3}$
Where $v_{f}$ is the velocity at C.
Then the translational kinetic energy is given as $K_{T}=\dfrac{1}{2}mv_{f}$
$\implies K_{T}=\dfrac{10mgh}{6}$
$\implies K_{T}=\dfrac{5mgh}{3}$
Similarly, the rotational kinetic energy is given as $K_{R}=\dfrac{I\omega^{2}}{2}$
$\implies K_{R}=\dfrac{mR^{2}}{4}\times \dfrac{1}{R^{2}}\times \dfrac{4gh}{3}$
$\implies K_{R}=\dfrac{mgh}{3}$
Taking the ratio between $K_{T}$ and $K_{R}$, we get,
$\dfrac{K_{T}}{K_{R}}=\dfrac{\dfrac{5mgh}{3}}{\dfrac{mgh}{3}}$
$\therefore \dfrac{K_{T}}{K_{R}}=\dfrac{5}{1}$

Hence the correct answer is option,\[B.5\].

Note:
Here, for simplification, we are considering the rough and the smooth surface independently. To solve this problem, one must know the radius of gyration of a solid cylinder. We must also be careful in the calculations.