Question

POQ is a line. Ray OR is a perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that\[\angle ROS = \dfrac{1}{2}(\angle QOS - \angle POS)\].

Answer 1

Hint: We will solve this problem by using a theorem about angles of linear pairs. This theorem states that the sum of angles of a linear pair is always equal to $180^\circ $. To solve this, we need to derive the equation for \[\angle ROS\] in terms of $\angle POS$ and $\angle QOS$ separately. And using both the equations we will prove \[\angle ROS = \dfrac{1}{2}(\angle QOS - \angle POS)\].

Complete step-by-step answer:
Representing the data of above question in the following diagram,

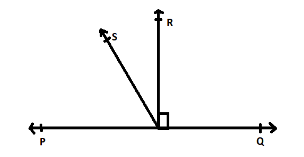
We are given with the data that,
$\overleftrightarrow {POQ}$ is a line.
$\overrightarrow {OR} \bot \overline {PQ} $
$\overrightarrow {OS} $lying between $\overrightarrow {OP} $and $\overrightarrow {OR} $
As $\overrightarrow {OR} \bot \overline {PQ} $
So that $\angle POR = 90^\circ $
Sum of angle in linear pair always equal to $180^\circ $
$\angle POS + \angle SOR + \angle QOR = 180^\circ $……….(1)
Putting $\angle QOR = 90^\circ $in equation (1)
$\angle POS + \angle SOR + 90^\circ = 180^\circ $
Taking 90degree to the right hand side we get,
$ \Rightarrow \angle POS + \angle SOR = 180^\circ - 90^\circ $
$ \Rightarrow \angle POS + \angle SOR = 90^\circ $
$ \Rightarrow \angle SOR = 90^\circ - \angle POS$………………(2)
From the figure we know that
$\angle QOR = 90^\circ $
Given that $\overrightarrow {OS} $lying between $\overrightarrow {OP} $and $\overrightarrow {OR} $
$\angle QOS - \angle ROS = 90^\circ $
$\angle ROS = \angle QOS - 90^\circ $……………..(3)
On adding equation (2) and (3) we get,
$2\angle ROS = \angle QOS - \angle POS$
Dividing both the sides by 2 we get,
$ \Rightarrow \angle ROS = \dfrac{1}{2}\angle QOS - \angle POS$
Hence it is proved that
$ \Rightarrow \angle ROS = \dfrac{1}{2}\angle QOS - \angle POS$

Note: Here angle ROS and angle SOR are the same. You might be mistaken the as different angle’
When we shift a term from one side to another, the sign of the term changes. For example + sign of left hand side becomes – in right hand side and vice versa. Similarly multiply sign becomes division sign and vice versa when we shift terms from left hand side to right hand side or do opposite.
The statement $\overrightarrow {OS} $ lying between $\overrightarrow {OP} $ and $\overrightarrow {OR} $ does not mean that the former ray divides the angle between later two rays into equal parts. You might be mistaken about that.
There is a difference between ray and line. Ray starts from one point and continues to the infinity while the line can go on to infinity in both directions.