Question

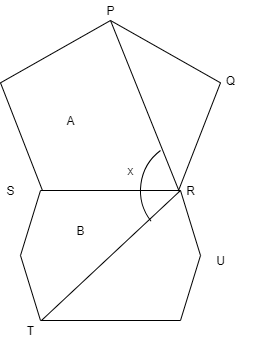
Polygon A is a regular pentagon while polygon B is a regular hexagon. Find \[\angle x\].

(a) \[{{108}^{0}}\]
(b) \[{{132}^{0}}\]
(c) \[{{124}^{0}}\]
(d) \[{{96}^{0}}\]

Answer 1

Hint: We solve this problem using simple geometry after finding the angle in pentagon and hexagon. We use the formula for finding the angle in regular polygon having \['n'\] sides is
\[\theta =\dfrac{\left( n-2 \right){{180}^{0}}}{n}\]. By using this formula we calculate the angle in both hexagon and pentagon and then by using simple geometry we find the value of \[\angle x\].

Complete step by step answer:
Let us divide the \[\angle x\] in two parts as \[\angle SRP\] and \[\angle SRT\]
Here we can write
\[\Rightarrow \angle x=\angle SRP+\angle SRT....equation(i)\]
Now let us take the pentagon and find the value of \[\angle SRP\].
We know that the angle in regular polygon having \['n'\] sides is \[\theta =\dfrac{\left( n-2 \right){{180}^{0}}}{n}\].
Now for a pentagon we take \[n=5\] then, we get
\[\begin{align}
  & \Rightarrow {{\theta }_{1}}=\dfrac{\left( 5-2 \right){{180}^{0}}}{5} \\
 & \Rightarrow {{\theta }_{1}}={{108}^{0}} \\
\end{align}\]
We know that for a regular polygon all the angles are equal.
So, we can write
\[\angle PQR=\angle QRS={{108}^{0}}\]
Now, let us consider the triangle \[\Delta PQR\]
We know that the sum of all angles in a triangle is \[{{180}^{0}}\]. By applying this to \[\Delta PQR\] we get
\[\Rightarrow \angle PQR+\angle QRP+\angle RPQ={{180}^{0}}\]
We know that \[PQ=QR\] so, opposite angles are also equal that is \[\angle QRP=\angle RPQ\]
By substituting these values in above equation we get
\[\begin{align}
  & \Rightarrow {{108}^{0}}+2\left( \angle QRP \right)={{180}^{0}} \\
 & \Rightarrow \angle QRP=\dfrac{{{72}^{0}}}{2}={{36}^{0}} \\
\end{align}\]
Now, let us consider \[\angle QRS\] and by dividing this angle in two parts we can write
\[\begin{align}
  & \Rightarrow \angle QRS=\angle SRP+\angle PRQ \\
 & \Rightarrow \angle SRP=\angle QRS-\angle PRQ \\
\end{align}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow \angle SRP={{108}^{0}}-{{36}^{0}} \\
 & \Rightarrow \angle SRP={{72}^{0}} \\
\end{align}\]
So, we got the first part.
Now, let us consider the hexagon and find the value of \[\angle SRT\].
We know that the angle in regular polygon having \['n'\] sides is \[\theta =\dfrac{\left( n-2 \right){{180}^{0}}}{n}\].
Now for a hexagon we take \[n=6\] then, we get
\[\begin{align}
  & \Rightarrow {{\theta }_{2}}=\dfrac{\left( 6-2 \right){{180}^{0}}}{6} \\
 & \Rightarrow {{\theta }_{2}}={{120}^{0}} \\
\end{align}\]
So, we can write \[\angle SRU={{120}^{0}}\]
We know that the diagonal of opposite vertices of the hexagon divides the angles at both vertices in equal parts, that is \[\angle SRT=\angle TRU\]. From this we can write
\[\Rightarrow \angle SRT=\dfrac{\angle SRU}{2}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow \angle SRT=\dfrac{{{120}^{0}}}{2} \\
 & \Rightarrow \angle SRT={{60}^{0}} \\
\end{align}\]
So, we have solved both the parts.
Now by substituting the required angles in equation (i) we get
\[\begin{align}
  & \Rightarrow \angle x=\angle SRP+\angle SRT \\
 & \Rightarrow \angle x={{72}^{0}}+{{60}^{0}} \\
 & \Rightarrow \angle x={{132}^{0}} \\
\end{align}\]
Therefore the value of \[\angle x\] is \[{{132}^{0}}\].

So, the correct answer is “Option b”.

Note: This problem can be solved in other ways.
We can write form the figure that
\[\begin{align}
  & \Rightarrow \angle QRU=\angle QRS+\angle SRU \\
 & \Rightarrow \angle QRU={{108}^{0}}+{{120}^{0}}={{228}^{0}} \\
\end{align}\]
The same angle can also be written as
\[\begin{align}
  & \Rightarrow \angle QRU=\angle QRP+\angle PRT+\angle TRU \\
 & \Rightarrow {{128}^{0}}={{36}^{0}}+x+{{60}^{0}} \\
 & \Rightarrow x={{132}^{0}} \\
\end{align}\]
So, option (b) is the correct answer.