Question

Points A \[(-1,y)\] and B \[(5,7)\] lie on a circle with center O \[(2,-3y)\]. find the values of y. Hence, find the radius of the circle.

Answer 1

Hint: Here, in this question it is given point O is the center and point A and B are the points on the circumference. we have to find the variable y and the radius of the circle for that we get need to use the condition that \[r=\sqrt{{{(x-g)}^{2}}+{{(y-f)}^{2}}}\]. And also use the condition that is \[OA=OB\] to find the variable y.

Complete step-by-step solution:
Here, in this question it is given that with point O \[(2,-3y)\] is the center then point A \[(-1,y)\] and B\[(5,7)\] lie on a circumference of the circle and consider radius is r.
Now, according to this question figure is given below:

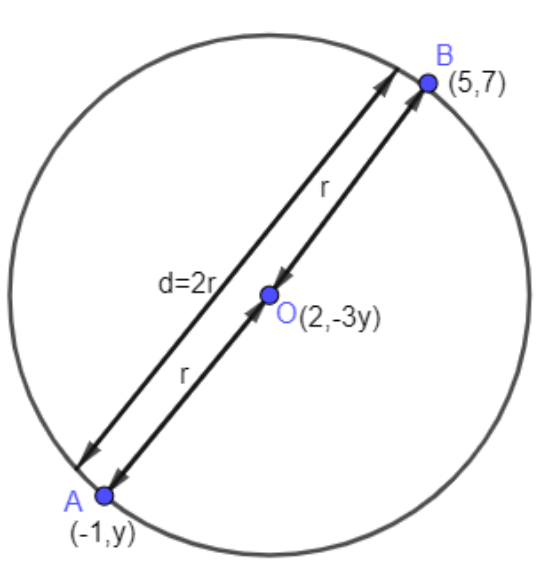
Now, in this figure we can see that the Radius \[=OA=OB\]
\[\Rightarrow OA=OB---(1)\]
We can find the value of OA by using the formula of \[r=\sqrt{{{(x-g)}^{2}}+{{(y-f)}^{2}}}\]
Where, g and f are the coordinates of center point O.
x and y are the coordinates which lies on the circumference point of the circle
Therefore, \[OA=\sqrt{{{(x-g)}^{2}}+{{(y-f)}^{2}}}\]
Here, by comparing the coordinates of point O \[(2,-3y)\equiv (g,f)\] we get the value of \[g=2\]and \[f=-3y\]
Similarly, by comparing the point A \[(-1,y)\equiv (x,y)\] we get \[x=-1\]and \[y=y\]
Therefore, \[OA=\sqrt{{{(-1-2)}^{2}}+{{(y-(-3y))}^{2}}}---(2)\]
Similarly, we can also find the value of \[OB\] that means \[OB=\sqrt{{{(x-g)}^{2}}+{{(y-f)}^{2}}}\]
Here, we have the value of \[g=2\] as well as \[f=-3y\]. The value of \[x=5\] as well as \[y=7\]. By substituting this value on above equation, we get:
\[OB=\sqrt{{{(5-2)}^{2}}+{{(7-(-3y))}^{2}}}---(3)\]
By substituting the value of equation (2) and (3) on equation (1) we get:
\[\Rightarrow \sqrt{{{(-1-2)}^{2}}+{{(y-(-3y))}^{2}}}=\sqrt{{{(5-2)}^{2}}+{{(7-(-3y))}^{2}}}\]
By squaring on both sides, we get:
\[\Rightarrow {{(-1-2)}^{2}}+{{(y-(-3y))}^{2}}={{(5-2)}^{2}}+{{(7-(-3y))}^{2}}\]
By simplifying further, we get:
\[\Rightarrow {{(-3)}^{2}}+{{(y+3y)}^{2}}={{(3)}^{2}}+{{(7+3y)}^{2}}\]
By further solving this above equation we get:
\[\Rightarrow 9+{{(y+3y)}^{2}}=9+{{(7+3y)}^{2}}\]
Here, 9 get cancelled on both sides we get:
\[\Rightarrow {{(y+3y)}^{2}}={{(7+3y)}^{2}}\]
By using the property of \[{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]on RHS we get:
\[\Rightarrow {{(4y)}^{2}}=49+42y+9{{y}^{2}}\]
By further solving this equation we get:
\[\Rightarrow 16{{y}^{2}}=49+42 y+9{{y}^{2}}\]
By rearranging this term, we get the quadratic equation:
\[\Rightarrow 7{{y}^{2}}-42y-49=0\]
We have to divide by 7 on both is sides we get:
\[\Rightarrow {{y}^{2}}-6y-7=0\]
We can solve this quadratic equation by using the factorisation method.
 \[\Rightarrow {{y}^{2}}+y-7y-7=0\]
By simplifying this we get:
\[\Rightarrow y(y+1)-7(y+1)=0\]
Here take \[(y+1)\] common in this above equation we get:
\[\Rightarrow (y+1)(y-7)=0\]
We have to equate each bracket to 0.
\[\Rightarrow (y+1)=0\] Or \[(y-7)=0\]
Therefore, we get:
\[\Rightarrow y=-1,7\]
When \[y=-1\] The coordinates of O, A and B are O \[(2,-3y)\], A \[(-1,y)\] and B\[(5,7)\]respectively.
\[\therefore \] \[\text{Radius}=OA=\sqrt{{{(-1-2)}^{2}}+{{(1-(-3\times 1))}^{2}}}\]
By simplifying this we get:
\[\Rightarrow \text{Radius}=OA=\sqrt{{{(3)}^{2}}+{{(1+3)}^{2}}}=\sqrt{9+16}\]
Therefore, we get
\[\Rightarrow \text{Radius}=OA=5\,\]
When \[y=7\] The coordinates of O, A and B are O\[(2,-3y)\], A\[(-1,y)\] and B\[(5,7)\] respectively.
\[\therefore \text{Radius}=OA=\sqrt{{{(-1-2)}^{2}}+{{(7-(-3\times 7))}^{2}}}\]
By simplifying this we get:
\[\Rightarrow \text{Radius}=OA=\sqrt{{{(3)}^{2}}+{{(7+21)}^{2}}}=\sqrt{9+784}\]
Therefore, we get
\[\Rightarrow \text{Radius}=OA=\sqrt{793}\,\]
Hence, for \[y=-1\] Radius is 5 and for \[y=7\] Radius is \[\sqrt{793}\].

Note: Whenever we face such types of questions the key concept here is to have a good understanding of the general equation of circle. The diagrammatic representation of the information provided helps in better understanding of the geometry involved to help getting on the right track to reach the solution.