Question

Point $P$ and $D$ are taken on the ellipse ${{\left( x+y-1 \right)}^{2}}+2{{\left( x+y-2 \right)}^{2}}=8$. If $a,b,c,d$ are lengths of the quadrilateral $PADB$ where $A$ and $B$ are foci of the ellipse. Then minimum value of ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}$\[\]
A. 12\[\]
B. 16\[\]
C. 30\[\]
D. None of these

Answer 1

Hint: Draw the diagram of the ellipse and the quadrilateral. Replace the linear expressions in the equation of ellipse with new variables. Then use the fact that the sum of distances from a point to the foci is twice semi-major axis. Finally, use the inequality between arithmetic mean and geometric mean to find the required.

Complete step-by-step answer:

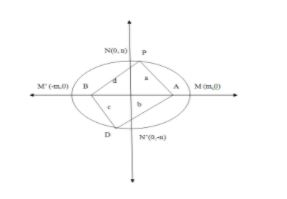
We have drawn the figure of the ellipse which cuts the coordinate axes at $M\left( m,0 \right),{{M}^{'}}\left( -m,0 \right),N\left( 0,n \right),{{N}^{'}}\left( 0,-n \right)$. The segment $M{{M}^{'}}$ is the major axis and $N{{N}^{'}}$ is the minor axis. The length of semi-major axis is the distance of either $M$ or ${{M}^{'}}$ from the origin that is $m$
As given in the question P and D are any two points on the ellipse. The foci of the ellipse on the major axis are named as A and B. The quadrilateral formed by joining the four points is PADB . We denote the lengths of the sides as $PA=a,AD=b,DB=c,PB=d$.
The given equation of ellipse is
\[{{\left( x+y-1 \right)}^{2}}+2{{\left( x+y-2 \right)}^{2}}=8...(1)\]
Let us substitute $x+y-1=X$ and $x+y-2=Y$as variables. We are replacing the combination variable with a single variable which will not change the shape of the ellipse. We know from the standard equation of ellipse with major-axis length $2m$ and minor axis length $2n$ that
\[\dfrac{{{x}^{2}}}{{{m}^{2}}}+\dfrac{{{y}^{2}}}{{{n}^{2}}}=1\]
We divide both side of equation (1) by 8 to convert it into above from,
\[\dfrac{{{X}^{2}}}{8}+\dfrac{{{Y}^{2}}}{4}=1\]
We also know from the property of ellipse that the sum of distances from to the two foci is constant and its value is $2m=2\left( 2\sqrt{2} \right)=4\sqrt{2}.$
Now P is a point on the ellipse whose sum of distances from the foci A and B is $PA+PB=a+d=4\sqrt{2}$ . Similarly the D is also a point on the ellipse whose sum of distances from the foci A and B is $DA+DB=b+c=4\sqrt{2}$. So
\[a+b+c+d=8\sqrt{2}\]
We use the inequality between arithmetic mean and geometric mean. Now,
\[\begin{align}
  & \dfrac{a+b+c+d}{4}\ge {{\left( abcd \right)}^{\dfrac{1}{4}}} \\
 & \Rightarrow \dfrac{8\sqrt{2}}{4}\ge {{\left( abcd \right)}^{\dfrac{1}{4}}} \\
 & \Rightarrow {{\left( 2\sqrt{2} \right)}^{4}}\ge abcd \\
 & \Rightarrow abcd\le 32 \\
\end{align}\]
So the maximum value of $abcd$ is 32. We again use the same inequality between means for ${{a}^{2}},{{b}^{2}},{{c}^{2}},{{d}^{2}}$ and have
\[\begin{align}
  & \dfrac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}}{4}\ge {{\left( {{a}^{2}}{{b}^{2}}{{c}^{2}}{{d}^{2}} \right)}^{\dfrac{1}{4}}}={{\left( abcd \right)}^{\dfrac{1}{2}}} \\
 & \Rightarrow \dfrac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}}{4}\ge {{\left( 32 \right)}^{\dfrac{1}{2}}}\left( \because abcd\le 32 \right) \\
 & \Rightarrow \dfrac{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}}{4}\ge 4\sqrt{2} \\
 & \Rightarrow {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}\ge 16\sqrt{2} \\
\end{align}\]
So the minimum value of ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}$ is $16\sqrt{2}$.

So, the correct answer is “Option D”.

Note: While solving this problem we need to take care of the fact that the sum of distance is twice semi-major axis not minor axis. We also see here that the substitution of new variables is possible because the expressions were linear.