Question

Point $\left( {3,2} \right)$ , $\left( { - 2, - 3} \right)$ and $\left( {2,3} \right)$ forms a/an _______ triangle.
A. Equilateral
B. Right angle
C. Isosceles
D. None of the above.

Answer 1

Hint: We can find the distance between the given points using the distance formula. Then we can compare them. If all the 3 points have equal distance between them, it will be an equilateral triangle. If only 2 sides are equal, then it will be isosceles and if the sum of the square of the 2 sides is equal to the square of the third side, it will be a right-angled triangle.

Complete step by step answer:

We are given 3 points. Let the points be A $\left( {3,2} \right)$ , B $\left( { - 2, - 3} \right)$ and C $\left( {2,3} \right)$
We know that distance between two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by,
 $d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
Now using this equation, we can find the distance between the points
The distance between A $\left( {3,2} \right)$ and B $\left( { - 2, - 3} \right)$ is
 $AB = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
On substituting the values, we get,
 $ \Rightarrow AB = \sqrt {{{\left( {3 + 2} \right)}^2} + {{\left( {2 + 3} \right)}^2}} $
On simplification we get,
 $ \Rightarrow AB = \sqrt {{5^2} + {5^2}} $
On squaring the terms in the root we get,
 $ \Rightarrow AB = \sqrt {25 + 25} $
On adding terms in root we get,
 $ \Rightarrow AB = \sqrt {50} $
On taking the squares, we get,
 $ \Rightarrow A{B^2} = 50$ … (1)

The distance between A $\left( {3,2} \right)$and C $\left( {2,3} \right)$is
 $AC = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
On substituting the values, we get,
 $ \Rightarrow AC = \sqrt {{{\left( {3 - 2} \right)}^2} + {{\left( {2 - 3} \right)}^2}} $
On simplification we get,
 $ \Rightarrow AC = \sqrt {{1^2} + {{\left( { - 1} \right)}^2}} $
On squaring terms given in root we get,
 $ \Rightarrow AC = \sqrt {1 + 1} $
On adding terms inside the root we get,
 \[ \Rightarrow AC = \sqrt 2 \]
On taking the square, we get,
 \[ \Rightarrow A{C^2} = 2\] … (2)

The distance between B $\left( { - 2, - 3} \right)$ and C $\left( {2,3} \right)$ is
 $ \Rightarrow BC = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
On substituting the values, we get,
 $ \Rightarrow BC = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( { - 3 - 3} \right)}^2}} $
On simplification we get,
 $ \Rightarrow BC = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 6} \right)}^2}} $
On squaring terms inside the root we get,
 $ \Rightarrow BC = \sqrt {16 + 36} $
On adding terms inside the root we get,
 $ \Rightarrow BC = \sqrt {52} $
On taking the square, we get,
 $ \Rightarrow B{C^2} = 52$… (3)

From (1), (2), and (3), we get,
 $A{B^2} + A{C^2} = 50 + 2$
 $ \Rightarrow A{B^2} + A{C^2} = 52$
 $ \Rightarrow A{B^2} + A{C^2} = B{C^2}$
Now we have the sum of the square of the 2 sides are equal to the square of the third side. So, by the converse of Pythagoras theorem, we can say that ABC is a right-angled triangle.
Therefore, the correct answer is option B.

Note: Alternate solution to this problem is given by
We can plot the points and compare the slopes.
So we can plot the given points and the lines joining them.

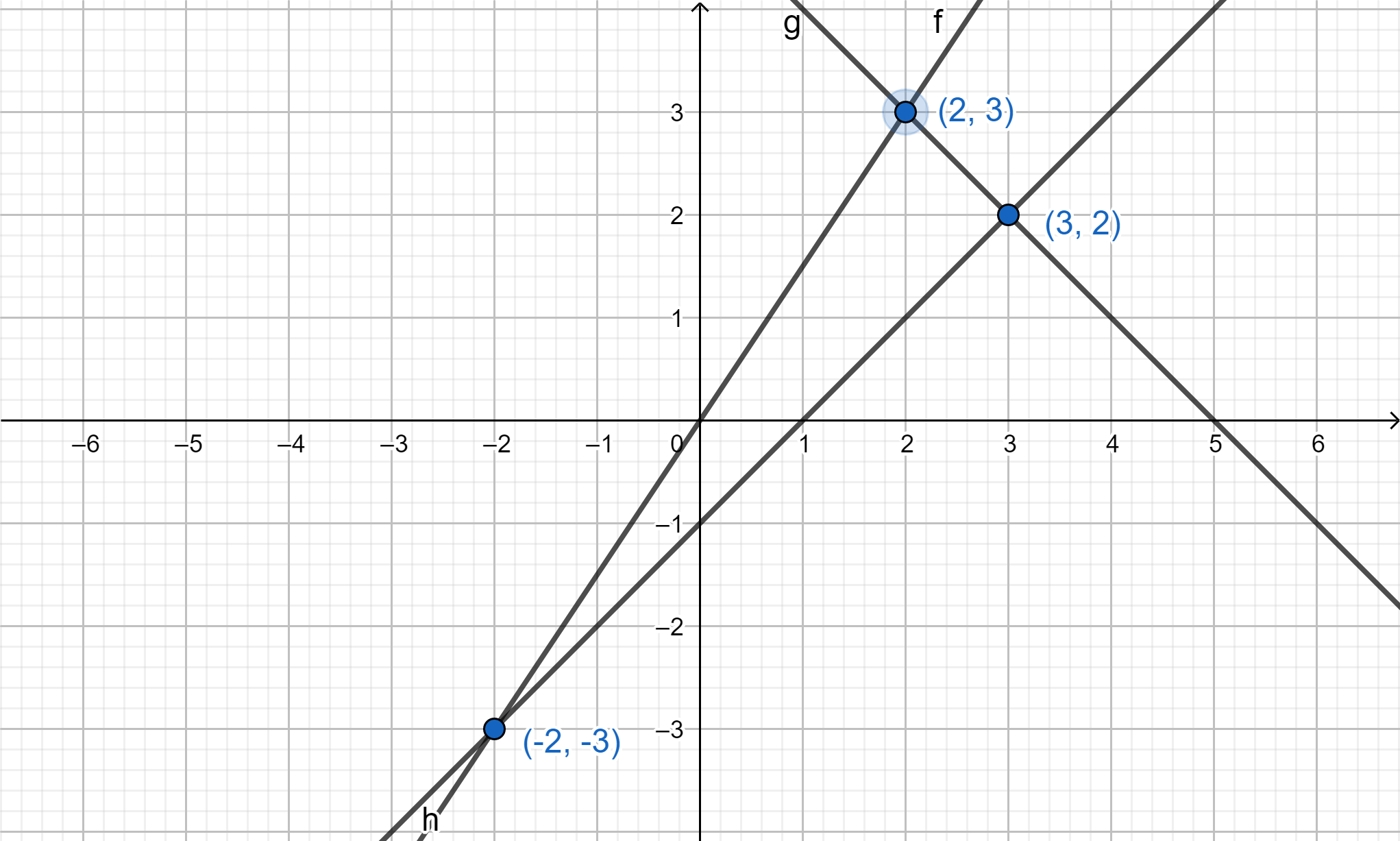
We know that slope of the line joining 2 points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by,
 $m = \dfrac{{\left( {{y_2} - {y_1}} \right)}}{{\left( {{x_2} - {x_1}} \right)}}$
The slope of line joining A $\left( {3,2} \right)$ and B $\left( { - 2, - 3} \right)$ is
 ${m_1} = \dfrac{{\left( { - 3 - 2} \right)}}{{\left( { - 2 - 3} \right)}}$
 $ \Rightarrow {m_1} = \dfrac{{ - 5}}{{ - 5}} = 1$
The slope of line joining A $\left( {3,2} \right)$ and C $\left( {2,3} \right)$ is
 ${m_2} = \dfrac{{\left( {3 - 2} \right)}}{{\left( {2 - 3} \right)}}$
 $ \Rightarrow {m_2} = \dfrac{1}{{ - 1}} = - 1$
We know that product of the slope of 2 perpendicular lines is equal to -1.
Now we can take the product of the slopes.
 ${m_1}{m_2} = 1 \times - 1 = - 1$
As the product of the slope is -1, the line AB and AC are perpendicular. So the line joining the points will give a right-angled triangle.