Question

How do you plot $ x + 2y = 8 $ using intercepts?

Answer 1

Hint: For linear equations do as follows:
I.Substitute $ 0 $ for $ y $ and then solve for $ x $ to find the $ x - $ intercept to plot the points in the graph.
II.Substitute $ 0 $ for $ x $ and then solve for $ y $ to find the $ y - $ intercept to plot the points in the graph.

Complete step-by-step answer:
 Given
Step1 –
The x-intercept is the value of $
  x \\
    \\
  $ when $ y $ = $ 0 $ .
The y-intercept is the value of y when $ x = 0 $ .
Step 2-
To get the x-intercept, let $ y = 0 $
Then substitute the values accordingly
 $
  x + (2 \times 0) = 8 \\
  x = 8 \;
  $
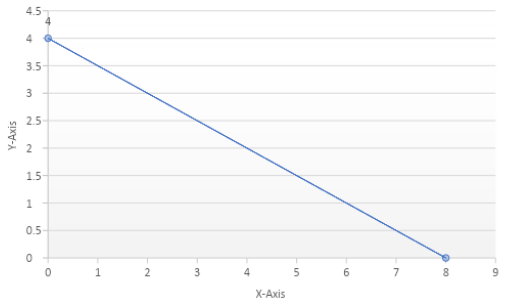
The x-intercept is (8,0)
To get the y-intercept, let $ x = 0 $
Then substitute the values accordingly
 $
  0 + 2y = 8 \\
  2y = 8 \\
  y = 4 \;
  $
The y-intercept is (0,4)
Therefore, the coordinates for the graph to be plotted are $ (0,4),(8,0) $
Step 4- Mark the points on the graph as shown below in Figure

Note: In the given question we can also find out the slope- intercept form i.e.,
 $ y = mx + b $ as shown below :
 $ 2y = 8 - x $ (subtract $ x $ from both sides)
 $ 2y = - x + 8 $ (rearrange the terms)
 $ y = \dfrac{{ - x + 8}}{2} $ (divide both sides by $ 2 $ to isolate y)
(break up the fraction)
(reduce)
Now, look at we can see that the equation is in the slope-intercept form i.e., $ y = mx + b $ where the slope $ (m) = - \dfrac{1}{2} $ and the y-intercept is $ b = 4 $ .
The given question does not require slope-intercept form and therefore we have not taken it out in the main solution.
From the above solution $ b = 4 $ tells us that the y-intercept of the given question is $ (0,4) $ and also, we need to remember that y-intercept is the point where the graph intersects with the y-axis (also shown the graph above)