Question

How do you plot the polar coordinate $ \left( {3,{{150}^ \circ }} \right) $ ?

Answer 1

Hint: As we know that the polar coordinate is like an alternative to the Cartesian coordinate system. On one hand the Cartesian system determines the position east and north of a fixed point while on the other hand the polar coordinates determine the location using direction and distance of a fixed point.

Complete step by step solution:
We first locate the angle of the polar coordinate plane and then we can plot the values.
As we know that a polar coordinate $ \left( {r,\theta } \right) $ in a Cartesian coordinate is $ \left( {r\cos \theta ,r\sin \theta } \right) $ .
So the value of $ \left( {3,{{150}^ \circ }} \right) $ in polar coordinate is $ \left( {3\cos {{150}^ \circ },3\sin {{150}^ \circ }} \right) $ .
Now, we know that the value of $ \cos {150^ \circ } $ as $ \left( { - \dfrac{{\sqrt 3 }}{2}} \right) $ and $ \sin {150^ \circ } $ is $ \left( {\dfrac{1}{2}} \right) $ .
So the Cartesian coordinate is $ \left( {3 \times \dfrac{{ - \sqrt 3 }}{2},3 \times \dfrac{1}{2}} \right) $ .
 $ \Rightarrow \left( {\dfrac{{ - 3\sqrt 3 }}{2},\dfrac{3}{2}} \right) $
 $ \Rightarrow \left( {\dfrac{{ - 3\sqrt 3 }}{2},\dfrac{3}{2}} \right) $
 $ \Rightarrow \left( { - 2.59807,1.5} \right) $
Hence we can plot these values as the polar coordinates.

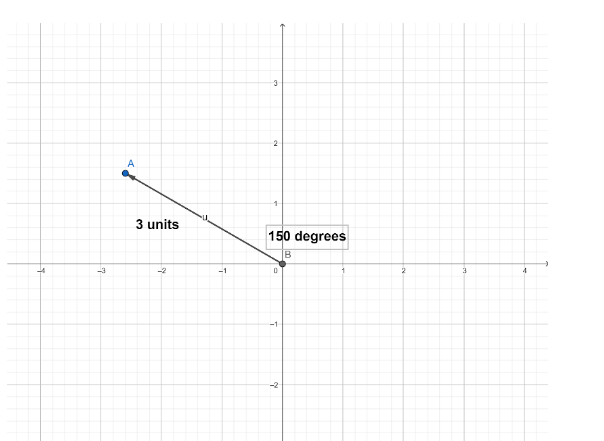
Note: We should note that in the above solution we have used the angle sum identity to find the values of $ \sin {150^ \circ } $ and $ \cos {150^ \circ } $ . We can write $ \sin {150^ \circ } $ as $ \sin \left( {{{180}^ \circ } - {{30}^ \circ }} \right) $ .
Also we know that $ \sin \left( {{{180}^ \circ } - \theta } \right) = \sin \theta $ . So, $ \sin \left( {{{180}^ \circ } - {{30}^ \circ }} \right) = \sin {30^ \circ } $ which gives us the value $ \sin {150^ \circ } = \dfrac{1}{2} $ .
Similarly we can find the value of $ \cos {150^ \circ } $ as it can be written as $ \cos \left( {{{180}^ \circ } - {{30}^ \circ }} \right) = - \cos {30^ \circ } $ . There is a negative sign in the cosine value. So, $ \cos {150^ \circ } = \dfrac{{ - \sqrt 3 }}{2} $ .