Question

Plot the points \[O(0,0)\] , \[A(2,2)\] and \[C(3,0)\] on graph paper and join these points. Name the type of triangle obtained and find its area.

Answer 1

Hint: According to the given question, firstly we will plot all the point on the graph that is \[O(0,0)\] , \[A(2,2)\] and \[C(3,0)\] all lies in first quadrant as x and y all are positive. So, you will mark all the given points and join them. Then, name the triangle formed that can be isosceles, scalene, equilateral or right angled triangle. Hence, find its area according to the triangle formed.

Formula used:
Here, we use the formula of area of triangle \[ = \dfrac{1}{2} \times base \times height\]

Complete step-by-step answer:
As the given points are \[O(0,0)\] , \[A(2,2)\] and \[C(3,0)\] .So, we must take a distance of 1 unit in both x and y axis .
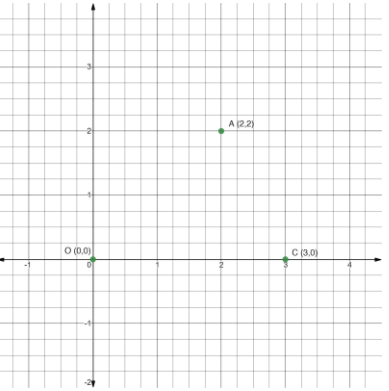
Firstly we will plot the graph, mark \[O(0,0)\] as 0 on the x axis and also 0 on the y axis which represents O. Then mark \[A(2,2)\] as 2 on the x axis and also 2 on the y axis which represents A.
And at last mark \[C(3,0)\] as 3 on the x axis and 0 on the y axis which represents C.
These points are shown in the graph below-

Now we will join the point O,A and C which will make a triangle as \[\Delta OAC\] shown in below figure-

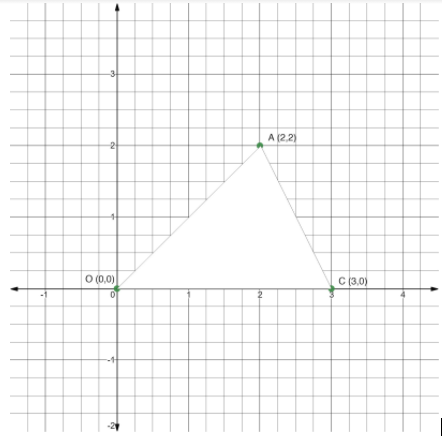
The triangle formed is isosceles triangles as two sides of a triangle are equal.
Now, we will calculate the area of triangle \[ = \dfrac{1}{2} \times base \times height\]
As, in \[\Delta OAC\] base \[ = 3\] units and height \[ = 2\] units
After substituting the values we get,
Area of triangle \[ = \dfrac{1}{2} \times 3 \times 2\]
Hence, the area of \[\Delta OAC\] \[ = 3\] sq. Units

Note: To solve these types of questions, we must have a knowledge of all the four quadrants and where the graph that is x and y both are positive, both are negative, x is positive and y is negative and x is negative and y is positive are situated in which quadrant. As well as you must know the formula of equilateral triangle that is \[\dfrac{{\sqrt 3 }}{4}sid{e^2}\] and the basic formula of area of triangle is \[\dfrac{1}{2} \times base \times height\]. It is important to observe the values to find an area formed from the graph itself.