Question

Plot the points $ A\left( 5,3 \right),B\left( -3,3 \right),C\left( -3,-4 \right),D\left( 5,-4 \right) $ and find the area of ABCD enclosed by the figure.

Answer 1

Hint: In this question, we will first draw a graph labeling the axis and origin. Then we will plot the given points where the first term represents the coordinate of the x-axis and the second term representing the coordinate of the y-axis. After plotting, we will notice that the formed shape is a rectangle. So then, we will calculate the length and breadth of the rectangle to calculate the area. Area of a rectangle with length l and breadth b is given by $ A=l\times b $

Complete step by step answer:
Here let us first plot the given point $ A\left( 5,3 \right),B\left( -3,3 \right),C\left( -3,-4 \right),D\left( 5,-4 \right) $ . For this, let us first draw axis on the graph paper and make the axis, origin and point. For point A(5,3) move five units to the right from origin and then move 3 places upwards.
For B(-3,3) move three units to the left from origin and then move 3 units upward.
For C(-3,-4) move three units to the left from origin and then move 4 units downwards.
For D(5,-4) move five units to the right from the origin and then move 4 units downwards.
After that, let us join the point A to B, B to C, C to D, and D to A.
Our graph looks like this,

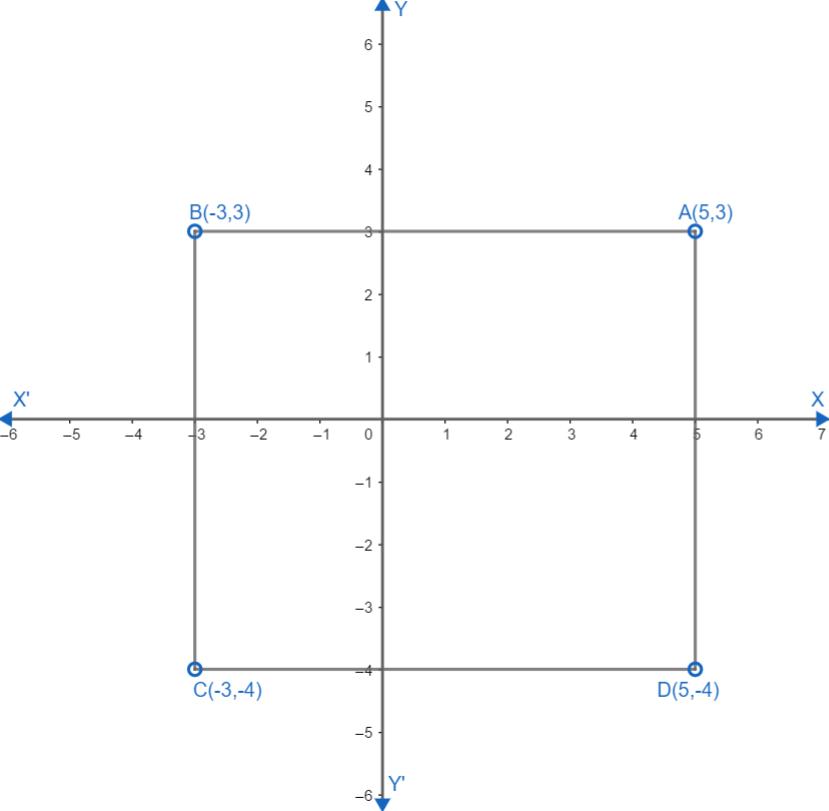
As we can see from the graph, the shape formed by joining these points is a rectangle. As we know that, the area of a rectangle of length l and breadth b is given by $ A=l\times b $ . So, let us first find the length and breadth of the figure obtained.
For this, we can just count units from the graph. As observed from the graph, the number of units between C and D is 8. Therefore, we can say that the length of the rectangle is 8 units. Also, we can see that the number of units between C and B are 7. Therefore, we can say that the breadth of the rectangle is 7 units. Hence, l = 8 units and b = 7 units.
So the area of the rectangle is $ l\times b $ .
 $ A=8\times 7 $ .
Hence area = 56 squared units.
Note:
 Students should plot the points carefully. For checking if it is a rectangle, students can measure all sides. For finding the length, students can also use the following formula, distance between two points $ \left( {{x}_{1}},{{y}_{1}} \right)\left( {{x}_{2}},{{y}_{2}} \right) $ is given by $ d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}} $ .