Question

Plot the points A(2,-3), B(-1,2) and C(0,-2) on graph paper. Draw the triangle formed by reflecting these points in the x axis. Are the two triangles congruent?

Answer 1

Hint: In this question, we will first plot the points given on the graph and form a triangle using them. After that, we will take reflection points in the x axis for all three points by changing signs of coordinate and obtain new points A', B' and C'. A'B'C' will also form a triangle. At last, we will use side-side-side (SSS) congruence condition to prove that two triangles are congruent.

Complete step-by-step answer:
 Let us now plot the points A(2,-3), B(-1,2) and C(0,-2) on graph paper. For point, A(2,-3) we will move 2 places on right side of x axis and then three places downward parallel to y axis and mark the point A. For point, B(-1,2) we will move 1 place on left side of x axis and then 2 places upwards and mark the point B. Similarly, for point (0,-2) as there is 0 as x coordinate, so we will just move 2 places on down side of y axis and mark point C. Join these three points to form a triangle. Now, we have to take reflection in the x axis, so, x coordinate will remain the same and we will change signs of y coordinates. New points obtained will be A'(2,3), B'(-1,-2) and C'(0,2).
We will mark these points too on the graph similarly we marked previous points and get the graph as below:

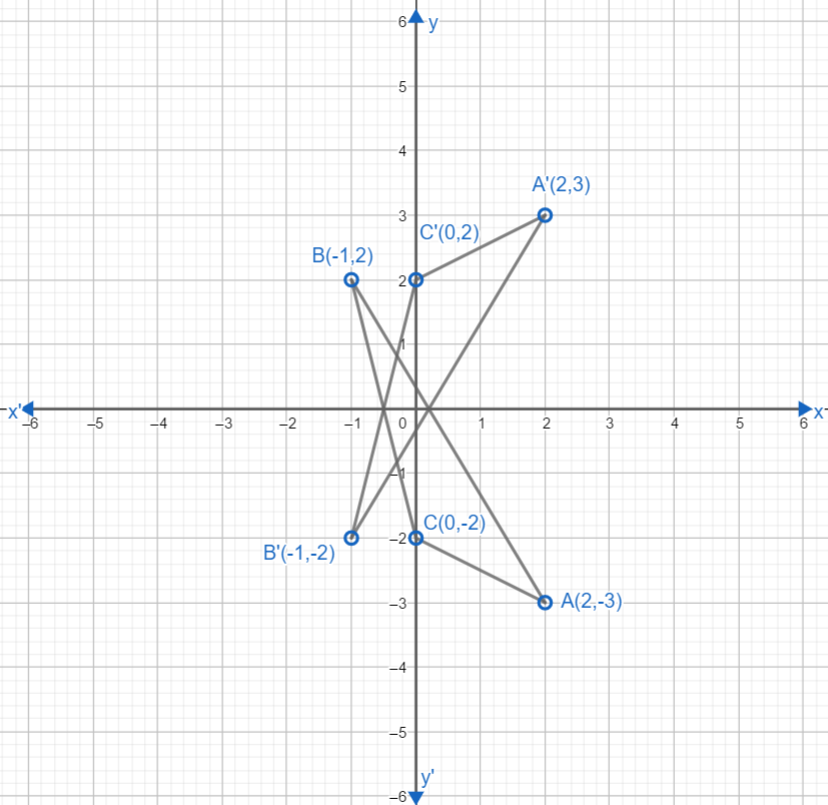
Now, we have two triangles $\Delta ABC\text{ and }\Delta A'B'C'$.
To check their congruence, let us measure the sides of both triangles.
Distance between two points is given by following formula: $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
Using it to find sides of triangle ABC, we get:
\[\begin{align}
  & AB=\sqrt{{{\left( -1-2 \right)}^{2}}+{{\left( 2+3 \right)}^{2}}}=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 5 \right)}^{2}}}=\sqrt{9+25}=\sqrt{34} \\
 & BC=\sqrt{{{\left( 0+1 \right)}^{2}}+{{\left( -2-2 \right)}^{2}}}=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{1+16}=\sqrt{17} \\
 & CA=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( -3+2 \right)}^{2}}}=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( -1 \right)}^{2}}}=\sqrt{4+1}=\sqrt{5} \\
\end{align}\]
Sides of triangle A'B'C' are
\[\begin{align}
  & A'B'=\sqrt{{{\left( -1-2 \right)}^{2}}+{{\left( -2-3 \right)}^{2}}}=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( -5 \right)}^{2}}}=\sqrt{9+25}=\sqrt{34} \\
 & B'C'=\sqrt{{{\left( 0+1 \right)}^{2}}+{{\left( 2+2 \right)}^{2}}}=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 4 \right)}^{2}}}=\sqrt{1+16}=\sqrt{17} \\
 & C'A'=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}}=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}}=\sqrt{4+1}=\sqrt{5} \\
\end{align}\]
As we can see,
\[\begin{align}
  & AB=A'B' \\
 & BC=B'C' \\
 & CA=C'A' \\
\end{align}\]
Hence, by side-side-side congruence condition triangles $\Delta ABC\text{ and }\Delta A'B'C'$ are congruent.
\[\Delta ABC\cong \Delta A'B'C'\]

Note: Students should carefully mark the points on the graph. While taking reflection on the x axis make sure that x coordinate remains same and signs of y coordinate are changed. Don't get confused if we were given reflection in y axis, then we had to change signs of x coordinate and y coordinate would remain the same. Carefully apply the congruence condition to prove if two triangles are congruent.