Question

How do you plot the point \[\left( { - 5,60^\circ } \right)\] on a polar graph?

Answer 1

Hint: In order to graph a point on the polar plane, you should find theta first and then locate r on that line. This approach allows you to narrow the location of a point to somewhere on one of the lines representing the angle. From there, you can simply count out from the pole the radial distance.

Complete step by step solution:
Change the radius from negative to positive by adding or subtracting (as appropriate) \[180^\circ \] to or from the angle.
Here, let us add \[180^\circ \] to the angle (instead of subtracting):
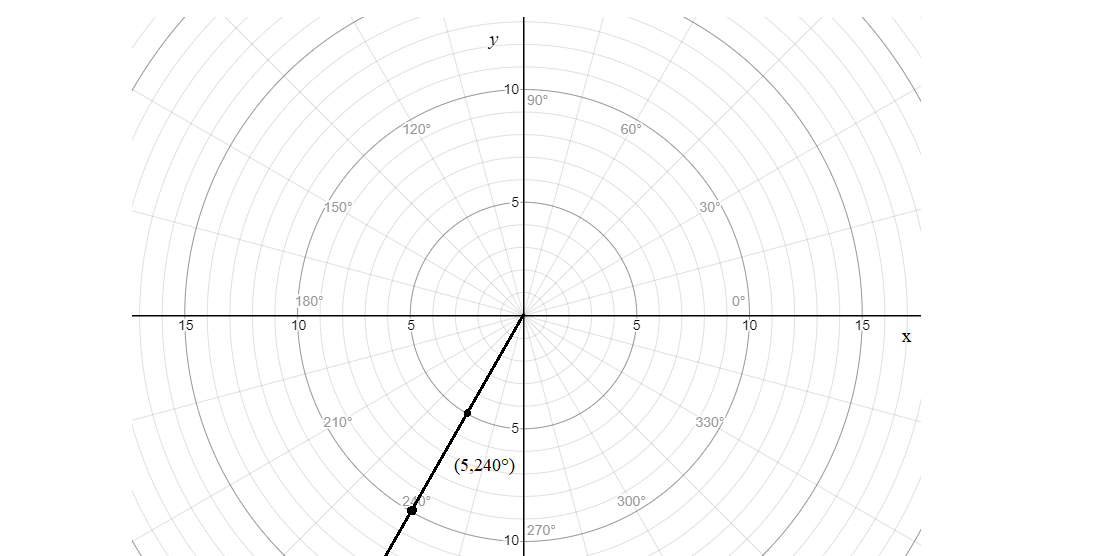
\[\left( { - 5,60^\circ } \right) \to \left( {5,240^\circ } \right)\]
Now, you merely find the intersection on the radius of 5 and the angle of \[240^\circ \] on the graph paper and draw a point as:
\[60^\circ = \dfrac{\pi }{3}\] and \[240^\circ = \dfrac{{4\pi }}{3}\] i.e., in graph we have: \[\left( { - 5,\dfrac{\pi }{3}} \right) \to \left( {5,\dfrac{{4\pi }}{3}} \right)\].

Additional information:
Identify the type of polar equation, the polar equation is in the form, \[r = a - b\cos \theta \]. Since the equation passes the test for symmetry to the polar axis, we only need to evaluate the equation over the interval \[\left[ {0,\pi } \right]\] and then reflect the graph about the polar axis.

Note: An angle whose measure is equal to 90 degrees is called a right angle, 180 degrees angle is called a straight angle and angles such as 270 degrees which are more than 180 but less than 360 degrees are called reflex angles. A 360 degrees angle is called a complete angle, hence by doing a complete rotation of two (or more) and adding or subtracting 360 degrees or a multiple of it before settling on the angle's terminal side, you can get an infinite number of angle measures, both positive and negative, for the same basic angle.