Question

Plot the following points in the cartesian plane whose x, y coordinates are given.

x	2	3	-10	-9	-4
y	-3	-3	41	10	-6

Answer 1

Hint: The x and y coordinates of the points have been given individually. We convert them in the form of $\left( x,y \right)$. The distances are from the origin. The x coordinate defines the distance of the point from the origin along the Y-axis. Same goes for y points. We plot those points in the graph according to their distance.

Complete step-by-step answer:
We have been provided with points on cartesian coordinates in the form of $\left( x,y \right)$.
Given all points will be turned into the form of $\left( x,y \right)$ where the distances are from the origin. The x coordinate defines the distance of the point from the origin along Y-axis.
The y coordinate defines the distance of the point from the origin along X-axis.
Now we plot all these points on the graph.

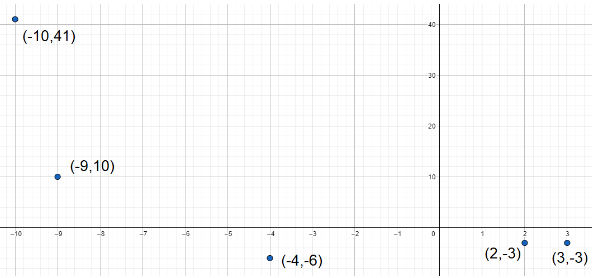
Let’s take every point one by one to find their positions. In every case we start from origin.
$\left( x,y \right)=\left( 2,-3 \right)$. Here, the x-distance is 2 units in a straight line along the X-axis from the Y-axis and the y-distance is 3 units in a straight line along the negative Y-axis from X axis.
$\left( x,y \right)=\left( 3,-3 \right)$. Here, the x-distance is 3 units in a straight line along the X-axis from the Y-axis and the y-distance is 3 units in a straight line along the negative Y-axis from X-axis.
$\left( x,y \right)=\left( -10,41 \right)$. Here, the x-distance is 10 units in a straight line along the negative X-axis from the Y-axis and the y-distance is 41 units in a straight line along the Y-axis from the X-axis.
$\left( x,y \right)=\left( -9,10 \right)$. Here, the x-distance is 9 units in a straight line along the negative X-axis from the Y-axis and the y-distance is 10 units in a straight line along the Y-axis from the X-axis.
$\left( x,y \right)=\left( -4,-6 \right)$. Here, the x-distance is 4 units in a straight line along the negative X-axis from the Y-axis and the y-distance is 6 units in a straight line along the negative Y-axis from the X-axis.

Note: We need to remember that the unit distance is fixed along both axes. Although we are finding the distance from origin, we are not finding the straight-line distance. For the straight-line distance, we have to apply Pythagoras’ theorem. We have a point $\left( x,y \right)$. Then the straight-line distance will be $\sqrt{{{x}^{2}}+{{y}^{2}}}$ unit.