Question

Plot the following points and check whether they are collinear or not:
A) $\left( {1,3} \right),\left( { - 1, - 1} \right),\left( { - 2, - 3} \right)$
B) $\left( {1,1} \right),\left( {2, - 3} \right),\left( { - 1, - 2} \right)$
C) $\left( {0,0} \right),\left( {2,2} \right),\left( {5,5} \right)$

Answer 1

Hint: For three points to be collinear means all three points lie on the straight line.
In the Cartesian plane, the horizontal line is the x-axis, and the vertical line is the y-axis. The x-axis and y-axis are perpendicular to each other.
The point where the x-axis and y-axis cut each other is called the origin, $\left( {0,0} \right)$ .
The coordinates of a point of the Cartesian plane is written in the form $\left( {x,y} \right)$.
Figure: Three collinear points
Therefore, Length AB + length BC = Length AC. Try to use this condition to check whether lines are collinear or not.
The length AB or distance between points A and B can be calculated using the distance formula.

Complete step-by-step answer:
Step 1: Distance formula for two points in the cartesian plane.
Let coordinates of a point A is $\left( {{x_1},{y_1}} \right)$ and a point B is $\left( {{x_2},{y_2}} \right)$ .
The distance between points A and B or the length AB is given by
$AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Step 2: Plot (A)
$\left( {1,3} \right),\left( { - 1, - 1} \right),\left( { - 2, - 3} \right)$

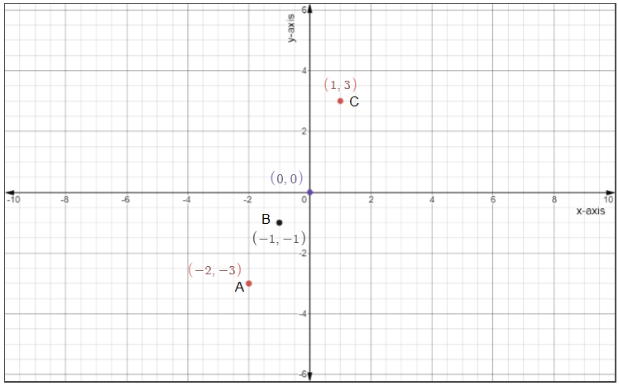
Step 3: Check for collinearity of (A)
Calculating length AB using the distance formula. $A\left( { - 2, - 3} \right);B\left( { - 1, - 1} \right)$
$
  AB = \sqrt {{{\left( { - 1 - \left( { - 2} \right)} \right)}^2} + {{\left( { - 1 - \left( { - 3} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 1 + 3} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 1 \right)}^2} + {{\left( 2 \right)}^2}} \\
   \Rightarrow \sqrt {1 + 4} \\
  \because AB = \sqrt 5 \\
 $
Calculating length BC using the distance formula. $B\left( { - 1, - 1} \right);C\left( {1,3} \right)$
\[
  BC = \sqrt {{{\left( {1 - \left( { - 1} \right)} \right)}^2} + {{\left( {3 - \left( { - 1} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( {3 + 1} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 2 \right)}^2} + {{\left( 4 \right)}^2}} \\
   \Rightarrow \sqrt {4 + 16} \\
   \Rightarrow \sqrt {20} \\
  \because BC = 2\sqrt 5 \\
 \]
Calculating length AC using the distance formula. $A\left( { - 2, - 3} \right);C\left( {1,3} \right)$
$
  AC = \sqrt {{{\left( {1 - \left( { - 2} \right)} \right)}^2} + {{\left( {3 - \left( { - 3} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( {1 + 2} \right)}^2} + {{\left( {3 + 3} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 3 \right)}^2} + {{\left( 6 \right)}^2}} \\
   \Rightarrow \sqrt {9 + 36} \\
   \Rightarrow \sqrt {9\left( {1 + 4} \right)} \\
  \because AC = 3\sqrt 5 \\
 $
AB + BC = $AB + BC = \sqrt 5 + 2\sqrt 5 = 3\sqrt 5 = AC$
$\because $hence, points A, B, C are collinear.
Step 4: Plot (B)
$\left( {1,1} \right),\left( {2, - 3} \right),\left( { - 1, - 2} \right)$

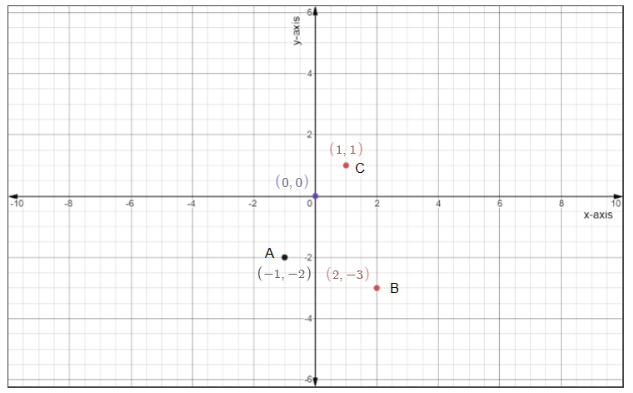
Step 5: Check for collinearity of (B)
Calculating length AB using the distance formula. $A\left( { - 1, - 2} \right);B\left( {2, - 3} \right)$
$
  AB = \sqrt {{{\left( {2 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 3 - \left( { - 2} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( {2 + 1} \right)}^2} + {{\left( { - 3 + 2} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 3 \right)}^2} + {{\left( { - 1} \right)}^2}} \\
   \Rightarrow \sqrt {9 + 1} \\
  \because AB = \sqrt {10} \\
 $
Calculating length BC using the distance formula. $B\left( {2, - 3} \right);C\left( {1,1} \right)$
\[
  BC = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {1 - \left( { - 3} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( { - 1} \right)}^2} + {{\left( {1 + 3} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( { - 1} \right)}^2} + {{\left( 4 \right)}^2}} \\
   \Rightarrow \sqrt {1 + 16} \\
  \because BC = \sqrt {17} \\
 \]
Calculating length AC using the distance formula. $A\left( { - 1, - 2} \right);C\left( {1,1} \right)$
$
  AC = \sqrt {{{\left( {1 - \left( { - 1} \right)} \right)}^2} + {{\left( {1 - \left( { - 2} \right)} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( {1 + 2} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 2 \right)}^2} + {{\left( 3 \right)}^2}} \\
   \Rightarrow \sqrt {4 + 9} \\
  \because AC = \sqrt {13} \\
 $
AB + BC = $AB + BC = \sqrt {10} + \sqrt {17} \ne AC = \sqrt {13} $
$\because $hence, points A, B, C are not collinear.
Step 6: Plot (C)
$\left( {0,0} \right),\left( {2,2} \right),\left( {5,5} \right)$

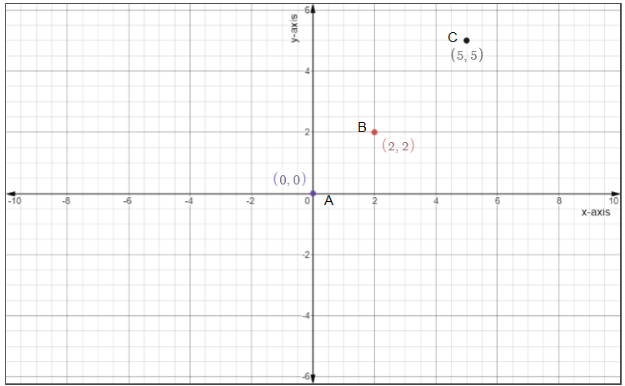
Step 7: Check for collinearity of (C)
Calculating length AB using the distance formula. $A\left( {0,0} \right);B\left( {2,2} \right)$
$
  AB = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {2 - 0} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}} \\
   \Rightarrow \sqrt {4 + 4} \\
  \because AB = 2\sqrt 2 \\
 $
Calculating length BC using the distance formula. $B\left( {2,2} \right);C\left( {5,5} \right)$
\[
  BC = \sqrt {{{\left( {5 - 2} \right)}^2} + {{\left( {5 - 2} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 3 \right)}^2} + {{\left( 3 \right)}^2}} \\
   \Rightarrow \sqrt {9 + 9} \\
  \because BC = 3\sqrt 2 \\
 \]
Calculating length AC using the distance formula. $A\left( {0,0} \right);C\left( {5,5} \right)$
$
  AC = \sqrt {{{\left( {5 - 0} \right)}^2} + {{\left( {5 - 0} \right)}^2}} \\
   \Rightarrow \sqrt {{{\left( 5 \right)}^2} + {{\left( 5 \right)}^2}} \\
   \Rightarrow \sqrt {25 + 25} \\
  \because AC = 5\sqrt 2 \\
 $
AB + BC = $AB + BC = 2\sqrt 2 + 3\sqrt 2 = 5\sqrt 2 = AC$
$\because $hence, points A, B, C are collinear.

Final answer: (A) and (C) are collinear but (B) is non-collinear.

Note: Distance formula for two points in the 3-dimensional cartesian plane.
Let coordinates of a point A is $\left( {{x_1},{y_1},{z_1}} \right)$ and a point B is $\left( {{x_2},{y_2},{z_2}} \right)$ .
The distance between points A and B or the length AB is given by
$AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $
The x-axis and y-axis divide the Cartesian plane into four parts, each part is known as a quadrant.
Pictorial representation of quadrants: