Question

Plot a graph for the equation \[y = {x^2} - 4x\].

Answer 1

Hint:
Here we need to plot the given equation. For that, we will first simplify the equation and after simplification, we will find that the given equation is the equation of an upward parabola and its vertex is not at the center. We will write the equation in standard form and from there, we will find the vertex of the parabola and then we will find the point of the curve with both the coordinates. After obtaining the points, we will plot the graph accordingly.

Complete step by step solution:
Here we need to plot the graph of the given equation \[y = {x^2} - 4x\].
We will first simplify the equation and we will write it in the standard form.
Now we will add 4 on both sides of the equation. Therefore, we get
\[ \Rightarrow y + 4 = {x^2} - 4x + 4\]
Rewriting the equation, we get
\[ \Rightarrow y + 4 = {x^2} - 2 \cdot 2 \cdot x + {2^2}\]
Using the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2 \cdot a \cdot b\], we get
\[ \Rightarrow y + 4 = {\left( {x - 2} \right)^2}\]
Rewriting the equation, we get
\[ \Rightarrow {\left( {x - 2} \right)^2} = y - \left( { - 4} \right)\] ………. \[\left( 1 \right)\]
We can see that the given equation is the equation of the upward parabola and it is a shifted parabola i.e. vertex is not at the center.
We know that the equation of shifted upward parabola is given by \[{\left( {x - h} \right)^2} = y - k\].
Here, vertex of this shifted upward parabola is \[\left( {h,k} \right)\].
Comparing this general equation with standard equation, we get the vertex of the shifted upward parabola as \[\left( {2, - 4} \right)\].
Now, we will first find the intersection of the parabola with \[x\] axis by the putting the value \[y = 0\] in the equation of the parabola i.e. in equation \[\left( 1 \right)\].
\[ \Rightarrow {\left( {x - 2} \right)^2} = 0 - \left( { - 4} \right)\]
On further simplification, we get
\[ \Rightarrow {\left( {x - 2} \right)^2} = 4\]
Now, taking square roots on both sides, we get
\[\begin{array}{l} \Rightarrow \sqrt {{{\left( {x - 2} \right)}^2}} = \sqrt 4 \\ \Rightarrow x - 2 = 2\end{array}\]
On adding 2 on both sides, we get
\[\begin{array}{l} \Rightarrow x - 2 + 2 = 2 + 2\\ \Rightarrow x = 4\end{array}\]
Therefore, point of intersection of the parabola with the \[x\] axis is equal to \[\left( {0,4} \right)\].
Similarly, we will first find the intersection of the parabola with \[y\] axis by the putting the value \[x = 0\] in the equation of the parabola i.e. in equation \[\left( 1 \right)\].
\[ \Rightarrow {\left( {0 - 2} \right)^2} = y - \left( { - 4} \right)\]
On further simplification, we get
\[ \Rightarrow 4 = y + 4\]
On subtracting 4 from both sides, we get
\[\begin{array}{l} \Rightarrow 4 - 4 = y + 4 - 4\\ \Rightarrow 0 = y\\ \Rightarrow y = 0\end{array}\]
Therefore, point of intersection of the parabola with the \[y\] axis is equal to \[\left( {0,0} \right)\]
Now, we will plot the graph using all these points.

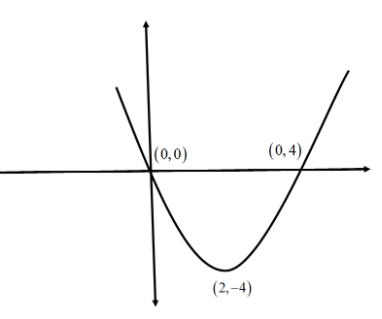
This is the required plot of the given equation.

Note:
The given equation is an equation of upward parabola. A parabola is a type of conic shape or a U-shaped plane curve in which any point is at an equal distance from a fixed point and from a fixed straight line known as the directrix. In order to plot any graph we always find the point of intersection of the graph with the coordinate axes.