
How do you plot $5i$ and find its absolute value?
Answer
556.2k+ views
Hint: In this question we have been given with a complex number which we will first represent in the general form of a complex number which is denoted as $a+bi$ where $a$ and $b$ are real numbers and $i$ is the imaginary part of the number which has the value $i=\sqrt{-1}$. The absolute value of the complex number can be found out using the formula $|z|=\sqrt{{{a}^{2}}+{{b}^{2}}}$where $z$ is the absolute value of the complex number.
Complete step by step answer:
We have the complex number given to us as $-5i$.
In this question we only have the imaginary part and no real part therefore, we will consider the value of the real part as $0$.
Therefore, the complex number can be represented in the general form $a+bi$ as $0-5i$, where the value of $a=0$ and $b=-5$.
Now to plot a complex number on the graph, the $x$ axis is considered to take the real part of the complex number and the $y$ axis takes the imaginary part of the number.
Therefore, the complex number in the form $a+bi$ is plotted as $(a,b)$.
Similarly, the complex number $0-5i$ will have coordinates as $(0,-5)$.
We can plot the point on the graph as:
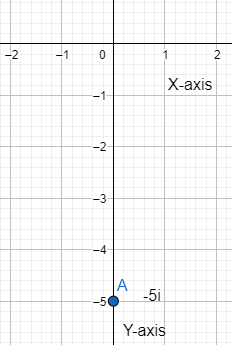
Where point $\text{A}$ denotes the complex number $0-5i$.
Now the absolute value of a complex number can be calculated using the formula $|z|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
On substituting the values of $a$ and $b$ in the formula, we get:
$|z|=\sqrt{{{0}^{2}}+{{(-5)}^{2}}}$
On squaring the terms and adding, we get:
$|z|=\sqrt{25}$
On taking the square root, we get:
$|z|=\pm 5$
Since we have to take the absolute value, we get:
$|z|=5$, which is the absolute value of the complex number.
Note: It is to be remembered that a square of a negative term is positive. The exponential form and the polar form of a complex number should be remembered while doing these types of sums. The modulus of the complex number is also called as the absolute value which gives the actual distance between the origin and the complex number. In the above sum it can be seen that the number has an absolute value of $5$ therefore it is $5$ units further from the origin.
Complete step by step answer:
We have the complex number given to us as $-5i$.
In this question we only have the imaginary part and no real part therefore, we will consider the value of the real part as $0$.
Therefore, the complex number can be represented in the general form $a+bi$ as $0-5i$, where the value of $a=0$ and $b=-5$.
Now to plot a complex number on the graph, the $x$ axis is considered to take the real part of the complex number and the $y$ axis takes the imaginary part of the number.
Therefore, the complex number in the form $a+bi$ is plotted as $(a,b)$.
Similarly, the complex number $0-5i$ will have coordinates as $(0,-5)$.
We can plot the point on the graph as:
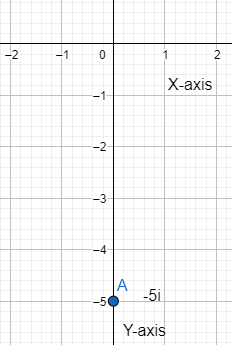
Where point $\text{A}$ denotes the complex number $0-5i$.
Now the absolute value of a complex number can be calculated using the formula $|z|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
On substituting the values of $a$ and $b$ in the formula, we get:
$|z|=\sqrt{{{0}^{2}}+{{(-5)}^{2}}}$
On squaring the terms and adding, we get:
$|z|=\sqrt{25}$
On taking the square root, we get:
$|z|=\pm 5$
Since we have to take the absolute value, we get:
$|z|=5$, which is the absolute value of the complex number.
Note: It is to be remembered that a square of a negative term is positive. The exponential form and the polar form of a complex number should be remembered while doing these types of sums. The modulus of the complex number is also called as the absolute value which gives the actual distance between the origin and the complex number. In the above sum it can be seen that the number has an absolute value of $5$ therefore it is $5$ units further from the origin.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




